- 古典概型与几何概型
- 共333题
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立。
(1)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(2)求该地3位车主中恰有1位车主甲、乙两种保险都不购买的概率。
正确答案
(1) 0.8;(2)0.384
解析
记A表示事件:该地的1位车主购买甲种保险:
B表示事件:该地的1位车主购买乙种保险但不购买甲种保险。
C表示事件:该地的1位车主至少购买甲、乙两种保险中的1种;
D表示事件:该地的1位车主甲、乙两种保险都不购买;
E表示事件:该地的3位车主中恰有1位车主甲、乙两种保险都不购买。
(1)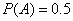
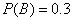
(2)D=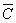
P(E)=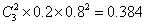
知识点
下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天。
(1)求此人到达当日空气质量优良的概率;
(2)求此人在该市停留时间只有1天空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结果不要求证明)
正确答案
见解析
解析
(1)在3月1日至3月13日这13天中,1日、2日、3日、7日、12日、13日共6天的空气质量优良,所以此人到达当日空气质量优良的概率是
(2)根据题意,事件“此人在该市停留期间只有1天空气重度污染”等价于“此人到达该市的日期是4日,或5日,或7日,或8日”。
所以此人在该市停留期间只有1天空气重度污染的概率为
(3)从3月5日开始连续三天的空气质量指数方差最大。
知识点
设



(1)求概率
(2)求

正确答案
(1)
解析
(1)若两条棱相交,则交点必为正方体8个顶点中的一个,过任意1个顶点恰有3条棱,
∴共有
∴ 
(2)若两条棱平行,则它们的距离为1或

∴ 

∴随机变量
∴其数学期望
知识点
从1,2,3,4,5中任意取出两个不同的数,其和为5的概率是__________。
正确答案
0.2
解析
该事件基本事件空间Ω={(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)}共有10个,记A=“其和为5”={(1,4),(2,3)}有2个,∴P(A)=
知识点
从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )。
正确答案
解析
由题意知总事件数为6,且分别为(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),满足条件的事件数是2,所以所求的概率为
知识点
某批次的某种灯泡共200个,对其寿命进行追踪调查,将结果列成频率分布表如下. 根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.
(1)根据频率分布表中的数据,写出a,b,c的值;
(2)某人从这200个灯泡中随机地购买了1个,求此灯泡恰好不是次品的概率;(3)某人从这批灯泡中随机地购买了
正确答案
见解析
解析
(1)解:


(2)解:设“此人购买的灯泡恰好不是次品”为事件
由表可知:这批灯泡中优等品有60个,正品有100个,次品有40个,
所以此人购买的灯泡恰好不是次品的概率为
(3)解:由(2)得这批灯泡中优等品、正品和次品的比例为
所以按分层抽样法,购买灯泡数 


知识点
海关对同时从A,B,C三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如右表所示. 工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
(1)求这6件样品中来自A,B,C各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
正确答案
见解析
解析
(1)因为工作人员是按分层抽样抽取商品,所以各地区抽取商品比例为:
所以各地区抽取商品数为:


(2)设各地区商品分别为:
基本时间空间

样本时间空间为:
所以这两件商品来自同一地区的概率为:
知识点
某校高三(1)班共有



(1)求分布表中

(2)王老师为完成一项研究,按学习时间用分层抽样的方法从这

(3)已知第一组学生中男、女生人数相同,在(2)的条件下抽取的第一组学生中,既有男生又有女生的概率是多少?
正确答案
见解析。
解析
(1)

(2)设应抽取


故应抽取2名第一组的学生,
(3)在(2)的条件下应抽取2名第一组的学生,记第一组中2名男生为

按时间用分层抽样的方法抽取2名第一组的学生共有

其中既有男生又有女生被抽中的有
所以既有男生又有女生被抽中的概率为
知识点
在3张奖券中有一、二等奖各1张,另1张无奖,甲、乙两人各抽取1张,两人都中奖的概率是______________;
正确答案
解析
基本事件的总数是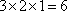
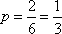
知识点
从




正确答案
解析
略
知识点
扫码查看完整答案与解析