- 向量的减法及其几何意义
- 共23题
1
题型:
单选题
|
已知


正确答案
D
解析
略
知识点
向量的减法及其几何意义
1
题型:填空题
|
正确答案
4
解析
略
知识点
向量的减法及其几何意义
1
题型:填空题
|
设平面区域




正确答案
见解析
解析
如11题解析图所示,可知题设平面区域
















即




知识点
向量的减法及其几何意义
1
题型:
单选题
|
定义域为






正确答案
C
解析
由题意知,点


由




由图象可知:
知识点
向量的减法及其几何意义
1
题型:填空题
|
在平面直角坐标系上,设不等式组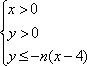
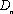
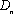
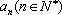

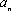
正确答案
6,6n
解析
第二问解析:由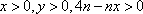
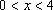
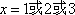
因此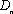
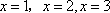
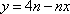
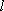
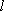
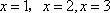
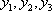
则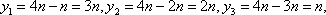
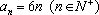
知识点
向量的减法及其几何意义
下一知识点 : 向量的三角形法则
扫码查看完整答案与解析

















