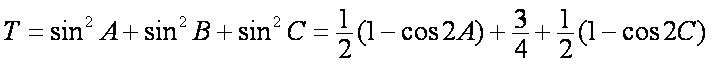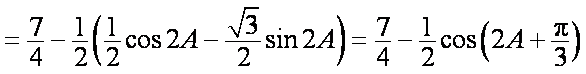- 分式不等式的解法
- 共109题
实数



正确答案
解析
略
知识点
已知实数


正确答案
解析
画图可知,四个角点分别是
知识点
对于


正确答案
解析
略
知识点
为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中
释放的浓度y(单位:毫克/立方米)随着时间
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之
和,由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用。
(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a(


正确答案
见解析。
解析
(1)因为一次喷洒4个单位的净化剂,
所以浓度
则当



当



综合得
(2)设从第一次喷洒起,经x(
浓度
因为

所以


令


知识点
设不等式
(1)求集合M;
(2)若

正确答案
见解析
解析
(1)①
②
① 
不等式的解集为
(2) 


知识点
已知



正确答案
4
解析
知识点
在△ABC中,角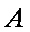
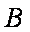
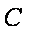
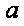
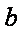
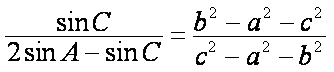
(1)求角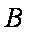
(2)设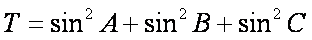
正确答案
见解析。
解析
(1)在△ABC中,
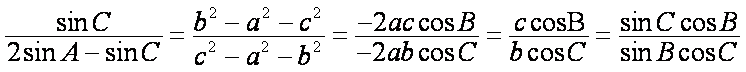
因为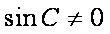
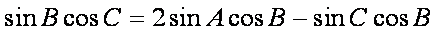
所以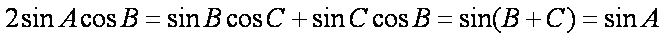
因为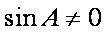
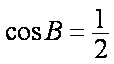
因为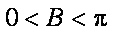
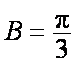
(2)
因为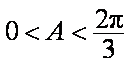
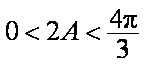
故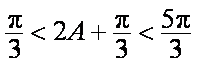
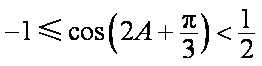
所以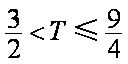
知识点
已知不等式
(1)解此关于x的不等式;
(2)若x=-

正确答案
见解析。
解析
(1)原式

①
②

③
-2<a<0时,





综上所述:


-2<





(2)∵x=-
∴

知识点
当实数



正确答案
解析
画出可行域,直线







知识点
已知函数

(1)求不等式
(2)若不等式

正确答案
见解析
解析
(1)由题意得
∴
所以

(2) 因为
所以
∴
所以


知识点
扫码查看完整答案与解析