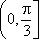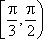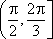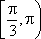- 一元高次不等式的解法
- 共24题
2.不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300名学生每周平均体育运动时间的样本数据(单位:小时)。
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12],估计该校学生每周平均体育运动时间超过4小时的概率;
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”。
附:K2=
正确答案
(1)90
(2)0.75
(3)95%
解析
(1)300×
(2)由频率分布直方图可得1﹣2×(0.100+0.025)=0.75,
∴该校学生每周平均体育运动时间超过4小时的概率为0.75;
(3)由(2)知,300位学生中有300×0.75=225人每周平均体育运动时间超过4小时,75人每周平均体育运动时间不超过4小时,又因为样本数据中有210份是关于男生的,90份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
∴K2=
∴有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”。
知识点
已知点


正确答案
-1
解析
知识点
若


正确答案
解析
略
知识点
已知函数f(x)=
正确答案
8或﹣2
解析
由题意可得当x>0时,令x﹣3=5,解得x=8符合题意;
当x≤0时,令x2+1=5,解得x=2,或x=﹣2,应取x=﹣2;
综上可得x=8或﹣2
知识点
设变量
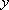
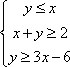
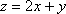
正确答案
解析
略
知识点
已
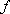
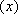
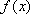
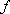
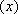
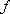
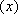
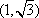
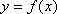
正确答案
解析
略
知识点
13.已知直线






正确答案
±2
解析
因为向量

【思路点拨】本题先由向量加法与减法的几何意义得到OA⊥OB,再由所给直线与圆的特殊性确定实数a的值.
知识点
已知两定点E(﹣2,0),F(2,0),动点P满足

(1)求曲线C的方程;
(2)过点D(0,﹣2)作直线l与曲线C交于A、B两点,点N满足
正确答案
见解析
解析
(1)∵动点P满足
∵E(﹣2,0),F(2,0),
∴点P的轨迹方程x2+y2=4
设M(x,y)是曲线C上任一点,∵PM⊥x轴,点M满足
∴P(x,2y)
∵点P的轨迹方程x2+y2=4
∴x2+4y2=4
∴求曲线C的方程是
(2)∵
当直线l的斜率不存在时,不符合题意;
当直线l的斜率存在时,设l:y=kx﹣2,l与椭圆交于A(x1,y1),B(x2,y2)
直线方程代入椭圆方程,可得(1+4k2)x2﹣16kx+12=0
∴x1+x2=
由△=256k2﹣48(1+4k2)>0,可得
∵
∴SOANB=2S△OAB=2|x1﹣x2|=
令k2=t,则




∴t=

∴k=
所求直线l的方程为

知识点
3.已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析