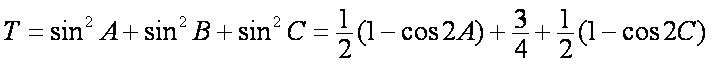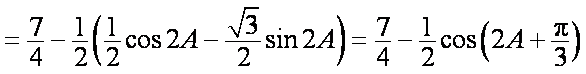- 分式不等式的解法
- 共109题
1
题型:简答题
|
设不等式
(1)求集合M;
(2)若

正确答案
见解析
解析
(1)①
②
① 
不等式的解集为
(2) 


知识点
分式不等式的解法
1
题型:填空题
|
已知



正确答案
4
解析
知识点
分式不等式的解法
1
题型:简答题
|
在△ABC中,角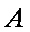
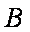
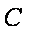
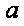
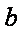
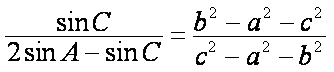
(1)求角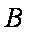
(2)设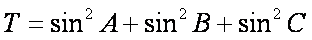
正确答案
见解析。
解析
(1)在△ABC中,
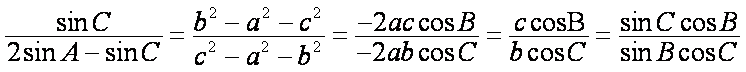
因为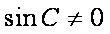
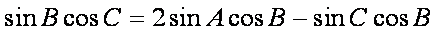
所以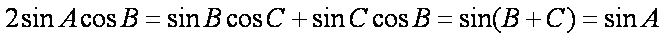
因为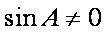
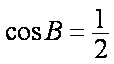
因为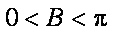
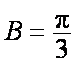
(2)
因为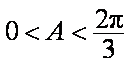
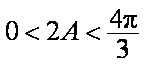
故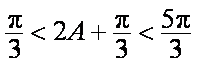
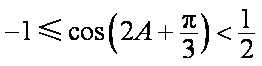
所以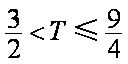
知识点
分式不等式的解法
1
题型:简答题
|
已知不等式
(1)解此关于x的不等式;
(2)若x=-

正确答案
见解析。
解析
(1)原式

①
②

③
-2<a<0时,





综上所述:


-2<





(2)∵x=-
∴

知识点
分式不等式的解法
1
题型:简答题
|
已知函数

(1)求不等式
(2)若不等式

正确答案
见解析
解析
(1)由题意得
∴
所以

(2) 因为
所以
∴
所以


知识点
分式不等式的解法
下一知识点 : 一元高次不等式的解法
扫码查看完整答案与解析