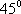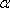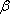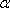- 平面与平面之间的位置关系
- 共19题
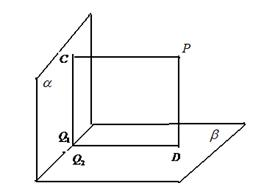
在空间中,过点
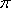
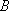
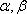
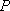
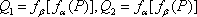
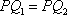
正确答案
解析
设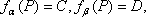
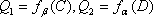
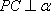
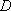
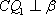
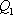
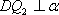
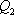
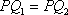
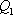
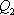
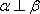
知识点
如图13,四棱锥PABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点。
正确答案
见解析。
解析
(1)证明:连接BD交AC于点O,连接EO.
因为ABCD为矩形,所以O为BD的中点。
又E为PD的中点,所以EO∥PB.
因为EO⊂平面AEC,PB⊄平面AEC,
所以PB∥平面AEC.
(2)
因为PA⊥平面ABCD,ABCD为矩形,
所以AB,AD,AP两两垂直。
知识点
如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
正确答案
解析
∵SD⊥底面ABCD,底面ABCD为正方形,
∴连接BD,则BD⊥AC,根据三垂线定理,可得AC⊥SB,故A正确;
∵AB∥CD,AB⊄平面SCD,CD⊂平面SCD,
∴AB∥平面SCD,故B正确;
∵SD⊥底面ABCD,
∠SAD是SA与平面SBD所成的角,∠SCD是SC与平面SBD所成的角,
而△SAD≌△SBD,
∴∠SAD=∠SCD,即SA与平面SBD所成的角等于SC与平面SBD所成的角,故C正确;
∵AB∥CD,∴AB与SC所成的角是∠SCD,DC与SA所成的角是∠SAB,
而这两个角显然不相等,故D不正确;
故选D。
知识点
3.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 正方体


且 
①
②MN//平面
③MN与
④点


⑤若点




其中有可能成立的结论为____________________。
正确答案
①②④④⑤
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析