- 匀速圆周运动
- 共72题
19.如图所示,在半径为R的水平圆盘中心轴正上方口处水平抛出一小球,圆盘以角速度ω作匀速转动,当圆盘半径ob恰好转到与初速度方向相同且平行的位置时,将小球抛出,要使球与圆盘只碰一次,且落点为b,重力加速度为g,小球抛点a距圆盘的高度^和小球的初速度v0可能应满足
正确答案
解析
小球做平抛运动,根据



考查方向
解题思路
圆盘转动的时间和小球平抛运动的时间相等,结合圆周运动的周期性求出时间的表达式,由
小球做平抛运动,小球在水平方向上做匀速直线运动,在竖直方向做自由落体运动,找出高度的表达式,根据水平位移和时间求出初速度的表达式,根据表达式分析确定。
易错点
忽略圆周运动的周期性,两个运动相碰时间相等。
知识点
3.如图所示为一种叫做“魔盘”的娱乐设施,当转盘转动很慢时,人会随着“磨盘”一起转动,当“魔盘”转动到一定速度时,人会“贴”在“魔盘”竖直壁上,而不会滑下。若磨盘半径为r,人与魔盘竖直壁间的动摩擦因数为μ,在人“贴”在“魔盘”竖直壁上,随“魔盘”一起运动过程中,则下列说法正确的是()
正确答案
解析
受力分析知分析性质力,所以没有向心力。A错误;
人在竖直方向受到重力和摩擦力,二力平衡,则知转速变大时,人与器壁之间的摩擦力不变.故B错误;
如果转速变大,由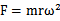
人恰好贴在魔盘上时,有 mg≤f, 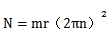
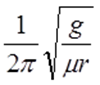
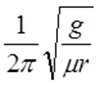
故选D
考查方向
解题思路
人随“魔盘”转动过程中受重力、弹力、摩擦力作用;由弹力提供圆周运动所需的向心力,由牛顿第二定律和向心力公式结合分析
易错点
人恰好贴在魔盘上时,有 mg≤f
知识点
4.儿童乐园里的游戏“空中飞椅”简化模型如图所示,座椅通过钢丝绳与顶端转盘连接.已知正常工作时转盘的转速一定。设绳长为L,绳与竖直方向夹角为θ,座椅中人的质量为m.则下列说法正确的是()
正确答案
解析
对“空中飞椅”受力分析得:


故选A。
考查方向
解题思路
合力提供向心力
易错点
匀速圆周运动,合力提供向心力是解题的关键。
知识点
2

正确答案
解析
A选项,明确小球离开轨道的条件:当小球与轨道压力小于零时;对小球进行受力分析,小球收重力,弹簧弹力,或者受到轨道的支持力,我们把这些力按沿着弹簧的方向和垂直于弹簧的方向分解,设重力与弹簧的夹角θ,有:mgcosθ+N=kΔx=mg,所以N= mg-mgcosθ≥0,当小球到最高点时,θ=0,N=0,当小球与轨道的压力一直存在时,小球不会脱离轨道,当压力为零时,小球在最高点,任然不会脱离轨道,故无论v0多大,小球均不会离开圆轨道,A选项正确,
B选项错误。
C选项,完成圆周运动的条件是:小球到最高点的时,所与的向心力






D选项,设小球在最高点时,受到轨道的压力为N1,最低点为N2,小球在最高点B点时合外力提供向心力:N1+mg-F弹力=








考查方向
1、考查圆周运动中向心力与速度的关系:F向心=,以及物体“刚好完成圆周运动”的物理条件:小球与轨道之间的压力为零,除此之外的力的合力刚好等于物体所需的向心力。
2、考查弹簧弹力与伸长量之间的关系。
3、考查能量的转化、功能关系及动能定理。
解题思路
1、首先根据弹簧弹力的公式:F=kx计算出弹簧的弹力,当小球与轨道压力为零时,求出小球在最高点D点的合外力,根据合外力提供向心力,计算出小球在D点所需的最小速度vD,只要小球在最高点速度大于等于小球在D点所需的最小速度vD,小球便能完成完整的圆周运动。
2、再根据动能定理公式计算出小球在最低点的最小速度v0:

3、根据动能定理与合外力提供向心力的公式计算小球在A、D两点对轨道的压力差。
易错点
1、对小球“能完成圆周运动”的物理条件不清楚。
2、对小球离开圆轨道的条件不清楚。
知识点
5.近年许多电视台推出户外有奖冲关的游戏节目,如图所示(俯视图)是某台设计的冲关活动中的一个环节。要求挑战者从平台A上跳到以O为转轴的快速旋转的水平转盘上而不落入水中。已知平台到转盘盘面的竖直高度为1.25 m,平台边缘到转盘边缘的水平距离为1 m,转盘半径为2m,以12.5 r/min的转速匀速转动,转盘边缘间隔均匀地固定有6个相同障碍桩,障碍桩及桩和桩之间的间隔对应的圆心角均相等。若某挑战者在如图所示时刻从平台边缘以水平速度沿 AO方向跳离平台,把人视为质点,不计桩的厚度,g取10 m/s2,则能穿过间隙跳上转盘的最小起跳速度为 ()
正确答案
解析
由图可知转盘间隙对应的圆心角θ=


考查方向
1、考查匀速圆周运动角速度的表达式:
2、考查平抛运动,运动的合成与分解。
解题思路
1、首先分析人所做运动的类型;根据平抛运动中运动的分解求解;只需要计算水平方向的运动。
2、根据角速度的表达式:ω=
3、根据平抛运动在水平方向上的计算公式:x=vt,计算出人的最小起跳速度。
易错点
1、对题意理解不清楚。
2、对人的运动类型分析不够清楚。
知识点
扫码查看完整答案与解析