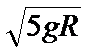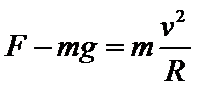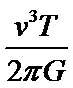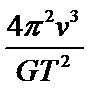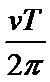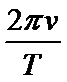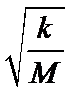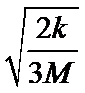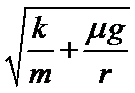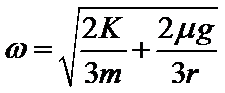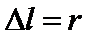- 匀速圆周运动
- 共72题
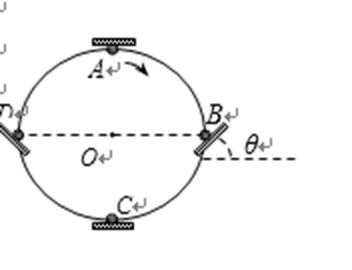
18.太极球是广大市民中较流行的一种健身器材。将太极球(拍和球)简化成如图所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做半径为R的匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势。A为圆周的最高点,C为最低点,B、D与圆心O等高。球的质量为m,重力加速度为g,则
正确答案
解析
A、设球运动的线速率为v,半径为R,则在A处时: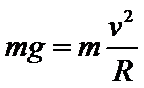
解得:F=2mg,即在C处板对球所需施加的力比A处大mg,故A错误;
B、球在运动过程中,动能不变,势能时刻变化,故机械能不守恒,故B错误;
C、球在任意时刻的速度大小相等,即球在最低点C的速度最小值为等于在最高点最小速度,根据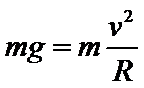
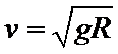
D、在B处合力提供向心力,即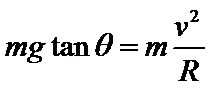
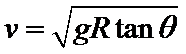
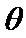
考查方向
解题思路
球在运动过程中受重力和支持力,由向心力公式可以求在各点的受力情况,并结合机械能守恒的条件分析即可。
易错点
抓住球在竖直面内始终不脱离板而做半径为R的匀速圆周运动,分析受力情况,注意合力提供小球运动的向心力。
知识点
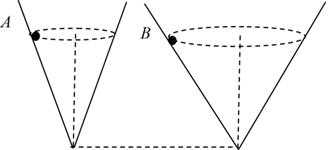
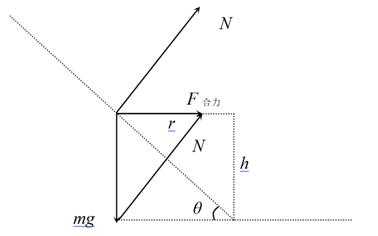
3.如图所示两个内壁光滑的倒立圆锥,底角不同,两个完全相同的小球A、B在两个圆锥内壁相同高度处分别做匀速圆周运动。关于小球A、B的运动情况,下列说法正确的是 ( )
正确答案
解析
A选项,如图所示,小球的受力图,合力F合力=mgtanθ=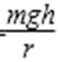
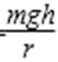
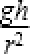
B选项,根据合外力提供向心力有: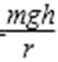
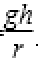
C选项,根据合外力提供向心力有: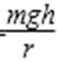
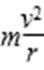
D选项,根据合外力提供向心力有:F向心力= F合力=mgtanθ=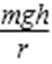
考查方向
解题思路
1、首先分析小球的受力情况,求出小球的合外力的表达式。2、根据合外力通过向心力分别求出,角速度,线速度,向心加速度的表达式,从而判断A、B小球角速度,线速度,向心加速度的大小关系。
易错点
1、对小球的受力分析不到位。2、对公式的选择模糊不清。
知识点
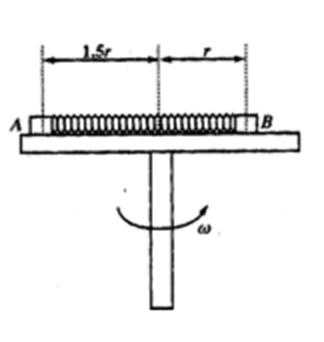
6.如图所示,水平转台上的小物体A、B通过轻弹簧连接,并随转台一起匀速转动,A、B的质量分别为m、2m,A、B与转台的动摩擦因数都为μ,A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,劲度系数为k,设本题中的最大静摩擦力等于滑动摩擦力,以下说法中正确的是( )
正确答案
解析
因为A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,所以弹簧伸长量为
由于A、B随转台一起匀速转动,可知角速度相同. A.当B受到的摩擦力为0时,弹簧弹力提供B的向心力,由牛顿第二定律得







考查方向
解题思路
由题意先计算出弹簧的形变量,然后根据A与B的相应条件,找出向心力,依据牛顿第二定律分析求解。
易错点
根据A与B的相应条件,关键进行正确的受力分析,找出在各自相应条件下的向心力。
知识点
6. 美国宇航局通过哈勃望远镜发现冥王星的“姐妹星” 鸟神星有一个小月亮,本次发现的鸟神星卫星具有重大意义,通过测量这颗小月亮的轨道,天文学家可以洞察它的演化,假设小月亮以速度v绕鸟神星做匀速圆周运动,测出运动的周期为T,已知引力常量为G,不计周围其他天体的影响,则下列说法正确的是( )
(在每小题给出的四个选项中,至少有一个选项是正确,全部选对的得6分,选对但不全的得3分,不选或有选错的得0分。)
正确答案
解析
A、C.根据圆周运动知识得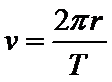
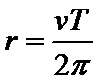
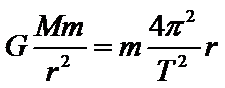
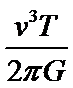
B.根据题意是小月亮围绕鸟神星做匀速圆周运动,根据万有引力定律仅题目已知条件无法求出小月亮的质量,故B错误;
D.根据向心加速度公式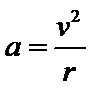
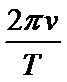
故本题选ACD
考查方向
解题思路
已知小月亮的线速度v与绕鸟神星的周期T,由圆周运动知识可得小月亮运动的轨道半径;根据万有引力提供向心力利用周期关系可解得鸟神星的质量,由圆周运动向心加速公式可解得小月亮的向心回速度值;
易错点
明确小月亮绕中心天体鸟神星做匀速圆周运动,因题目已知条件无法解得小月亮的质量。
知识点
8. 如图所示,有一水平转台,上面放置着用轻质弹簧连接的小物体A、B使其随转台一起匀速转动,A、B的质量分别为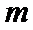
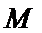
(在每小题给出的四个选项中,至少有一个选项是正确,全部选对的得6分,选对但不全的得3分,不选或有选错的得0分。)
正确答案
解析
因为A、B离转台中心的距离分别为1.5r、r,已知弹簧的原长为1.5r,所以弹簧伸长量为
由于A、B随转台一起匀速转动,可知角速度相同.
A.当B受到的摩擦力为0时,弹簧弹力提供B的向心力,由牛顿第二定律得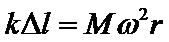
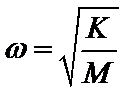
B. 当A受到的摩擦力为0时, 弹簧弹力提供A的向心力,由牛顿第二定律得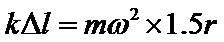
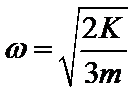
C. 当B刚好要滑动时,对B由摩擦力与弹簧弹力提供向心力,由牛顿第二定律得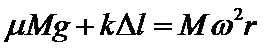
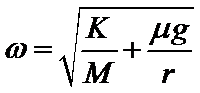
D. 当A刚好要滑动时对A由摩擦力与弹簧弹力提供向心力,由牛顿第二定律得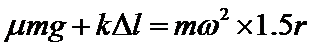
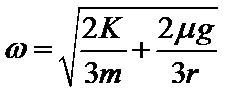
考查方向
解题思路
由题意先计算出弹簧的形变量,然后根据A与B的相应条件,找出向心力,依据牛顿第二定律分析求解。
易错点
根据A与B的相应条件,关键进行正确的受力分析,找出在各自相应条件下的向心力。
知识点
扫码查看完整答案与解析