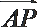- 平面向量
- 共1072题
21.如图,圆







(1)求动点

(2)过点







正确答案
(1)设

所以
又P在圆
所以
即
即
轨迹是以

长轴长为4的椭圆
(2)方法一:当直线

设直线

代入椭圆方程得:
△
设
则
由
所以
由(*)、(**)
解得

所以
即所求直线方程为:
解析
解析已在路上飞奔,马上就到!
知识点
7.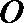
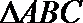
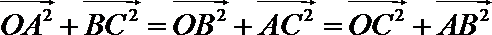
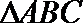
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,平行四边形ABCD中,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在∆ABC中,已知D是AB边上一点,若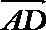
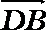
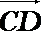
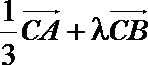
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
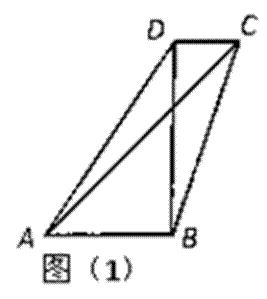
15.如图(1),在四边形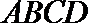
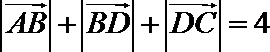
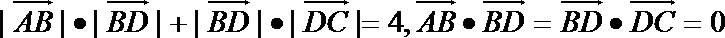
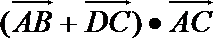
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
9.设点






正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
11.如图,抛物线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在△ABC中,已知向量
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,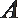
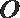
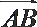
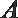
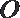
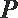
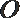
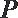
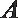
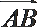
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知抛物线





(1)求证:


(2)设


正确答案
解:(1)设直线的方程为:
联立方程可得

设





而

即


(2)由


即得:

由(1)中②代入得

解析
解析已在路上飞奔,马上就到!
知识点
20. 已知点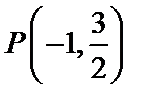
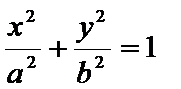

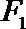
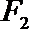
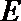
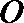
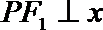
(1)求椭圆
(2)设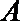
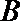
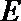


正确答案
解:(1)∵PF1⊥x轴,
∴F1(-1,0),c=1,F2(1,0),
|PF2|=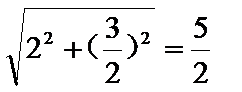
椭圆E的方程为:
(2)设A(x1,y1)、B(x2,y2),由 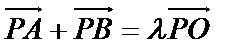
(x1+1,y1-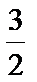
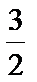
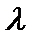
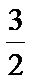
所以x1+x2=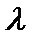
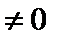
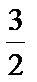
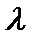
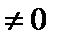
又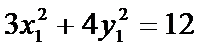
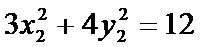
两式相减得3(x1+x2)(x1-x2)+ 4(y1+y2)(y1-y2)=0………..②
以①式代入可得AB的斜率k=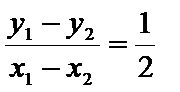
解析
解析已在路上飞奔,马上就到!
知识点
15.在△ABC和△AEF中,B是EF的中点,AB=EF=1,BC=6,



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.O是


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析