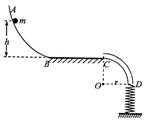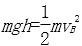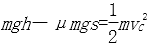- 牛顿运动定律的综合应用
- 共404题
光滑圆轨道和两倾斜直轨道组成如图所示装置,其中直轨道bc粗糙,直轨道cd光滑,两轨道相接处为一很小的圆弧。质量为m=0.1kg的滑块(可视为质点)在圆轨道上做圆周运动,到达轨道最高点a时的速度大小为v=4m/s,当滑块运动到圆轨道与直轨道bc的相切处b时,脱离圆轨道开始沿倾斜直轨道bc滑行,到达轨道cd上的d点时速度为零。若滑块变换轨道瞬间的能量损失可忽略不计,已知圆轨道的半径为R=0.25m,直轨道bc的倾角
(1)滑块在圆轨道最高点a时对轨道的压力大小;
(2)滑块与直轨道bc问的动摩擦因数;
(3)滑块在直轨道bc上能够运动的时间。
正确答案
(1)5.4N
(2)0.8
(3)7.66s
解析
(1)在圆轨道最高点a处对滑块由牛顿第二定律得:
∴
由牛顿第三定律得滑块在圆轨道最高点a时对轨道的压力大小为5.4N
(2) 从a点到d点全程由动能定理得:

(3)设滑块在bc上向下滑动的加速度为a1,时间为t1,向上滑动的加速度为a2,时间为t2;在c点时的速度为vc。
由c到d:

a点到b点的过程:
∴
在轨道bc上:
下滑:

上滑:


∵
滑块在两个斜面上运动的总时间:

知识点
传送带被广泛应用于各行各业。由于不同的物体与传送带之间的动摩擦因数不同,物体在传送带上的运动情况也有所不同。如图所示,一倾斜放置的传送带与水平面的倾角θ=370,在电动机的带动下以v=2m/s的速率顺时针方向匀速运行。M、N为传送带的两个端点,MN两点间的距离L=7m。N端有一离传送带很近的挡板P可将传送带上的物块挡住。在传送带上的O处先后由静止释放金属块A和木块B,金属块与木块质量均为1kg,且均可视为质点,OM间距离L=3m。sin37° = 0.6,cos37°=0.8,g取10m/s2。传送带与轮子间无相对滑动,不计轮轴处的摩擦。
(1)金属块A由静止释放后沿传送带向上运动,经过2s到达M端,求金属块与传送带间的动摩擦因数μ1。
(2)木块B由静止释放后沿传送带向下运动,并与挡板P发生碰撞。已知碰撞时间极短,木块B与挡板P碰撞前后速度大小不变,木块B与传送带间的动摩擦因数μ2=0.5。求:
a.与挡板P第一次碰撞后,木块B所达到的最高位置与挡板P的距离;
b.经过足够长时间,电动机的输出功率恒定,求此时电动机的输出功率。
正确答案
见解析。
解析
(1)金属块A在传送带方向上受摩擦力和重力的下滑分力,先做匀加速运动,并设其速度能达到传送带的速度v=2m/s,然后做匀速运动,达到M点。
金属块由O运动到M有 

且 t1+t2=t 即 t1+t2=2 ②
v=at1 即 2=at1 ③………1分
根据牛顿第二定律有 
由①②③式解得 t1=1s<t=2s 符合题设要求,加速度a=2m/s2
由①式解得金属块与传送带间的动摩擦因数μ1=1
(2)a. 由静止释放后,木块B沿传送带向下做匀加速运动,其加速度为a1,运动距离LON=4m,第一次与P碰撞前的速度为v1


与挡板P第一次碰撞后,木块B以速度v1被反弹,先沿传送带向上以加速度a2做匀减速运动直到速度为v,此过程运动距离为s1;之后以加速度a1继续做匀减速运动直到速度为0,此时上升到最高点,此过程运动距离为s2。



因此与挡板P第一次碰撞后,木块B所达到的最高位置与挡板P的距离
b. 木块B上升到最高点后,沿传送带以加速度a1向下做匀加速运动,与挡板P发生第二次碰撞,碰撞前的速度为v2

与挡板第二次碰撞后,木块B以速度v2被反弹,先沿传送带向上以加速度a2做匀减速运动直到速度为v,此过程运动距离为s3;之后以加速度a1继续做匀减速运动直到速度为0,此时上升到最高点,此过程运动距离为s4。


木块B上升到最高点后,沿传送带以加速度a1向下做匀加速运动,与挡板P发生第三次碰撞,碰撞前的速度为v3

与挡板第三次碰撞后,木块B以速度v3被反弹,先沿传送带向上以加速度a2做匀减速运动直到速度为v,此过程运动距离为s5;之后以加速度a1继续做匀减速运动直到速度为0,此时上升到最高点,此过程运动距离为s6。


以此类推,经过多次碰撞后木块B以2m/s的速度被反弹,在距N点1m的范围内不断以加速度a2做向上的减速运动和向下的加速运动。
木块B对传送带有一与传送带运动方向相反的阻力

故电动机的输出功率
解得P=8w
知识点
如图,斜面体的上表面除AB段粗糙外,其余部分光滑。一物体从斜面的顶端滑下,经过A、C两点时的速度相等,已知AB=BC,物体与AB段的动摩擦因数处处相等,斜面体始终静止在地面上,则 ( )
正确答案
解析
略
知识点
如图所示,车厢的质量为M,长度为L,静止在光滑水平面上。质量为m的木块(可看成质点)以速度

正确答案
解析
木块与车前壁碰撞过程中,木块和车厢组成的系统动量守恒
碰撞后,设车厢的速度大小为
解得
设经达时间t,木块将与车后壁相碰,由运动学公式得:
解得:
知识点
如图,将质量m=2kg的圆环套在与水平面成θ=37°角的足够长直杆上,直杆固定不动,环的直径略大于杆的截面直径,杆上依次有三点A、B、C,sAB=8m,sBC=0.6m,环与杆间动摩擦因数μ=0.5,对环施加一个与杆成37°斜向上的拉力F,使环从A点由静止开始沿杆向上运动,已知t=4s时环到达B点。试求:(重力加速度g=l0m/s2,sin37°=0.6,cos37°=0.8)
(1)F的大小;
(2)若到达B点时撤去力F,则环到达C点所用的时间。
正确答案
见解析
解析
(1)环做匀加速运动,
若Fsin370<Gcos370,杆对环的弹力在垂直杆向上,N+Fsin37°=mg cos37°,Fcos37°-μN-mg sin37°=ma,代入数据得,F=20N
若Fsin370>Gcos370,杆对环的弹力在垂直杆向下,N+mg cos37°=Fsin37°
Fcos37°-μN-mg sin37°=ma,代入数据得,F=12N。不符合要求。
(2)


若物体向下经过C点,mgsinθ-μmgcosθ=ma3,a3= gsinθ-μgcosθ=2m/s2,


知识点
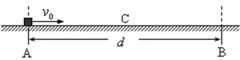
如图所示,质量为m带电量为+q的小滑块以大小为v0的初速度从A点进入宽度为d的AB绝缘水平面。当滑块运动至中点C时,速度大小为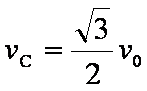
正确答案
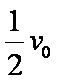
解析
略
知识点
一质量为m=2kg的滑块能在倾角为θ=300的足够长的斜面上以a=2.5m/s2匀加速下滑。如图所示,若用一水平推力F作用于滑块,使之由静止开始在t=2s内能沿斜面运动位移s=4m。求:(取g=10m/s2)
(1)滑块和斜面之间的动摩擦因数μ;
(2)推力F的大小。
正确答案
见解析
解析
(1)根据牛顿第二定律可得:mgsin300—μmgcos300=ma
(2)使滑块沿斜面做匀加速直线运动,有加速度向上和向下两种可能。
当加速度沿斜面向上时,F cos300—mgsin300—μ(F sin300+ mgcos300) =ma
代入数据得:
当加速度沿斜面向下时,mgsin300—F cos300—μ(F sin300+ mgcos300) =ma
代入数据得:
知识点
已知小孩与雪橇的总质量为m = 20 kg ,静止于水平冰面上,雪橇与冰面间的动摩擦因数为
(1)大人用F1=30N的水平恒力推雪橇,求经过4s秒雪橇运动的距离L;
(2)如图所示,若大人用大小为F2=50N,与水平方向成37°角的恒力斜向上拉雪橇,使雪橇由静止开始运动1m,之后撤去拉力,求小孩与雪橇在冰面上滑行的总距离。
正确答案
见解析。
解析
(1)对小孩进行受力分析,由牛顿第二定律得

解得 a = 0.5m/s2
根据运动学公式L = 
解得 L = 4 m
(2)小孩与雪橇先做匀加速直线运动,所受摩擦力为f1,运动的距离为s1


解得:f1= 17N
之后小孩与雪橇做匀减速直线运动,所受摩擦力为f2,运动的距离为S2


解得 f2= 20N
由动能定理有 
解得 S2=1.15 m
小孩与雪橇在冰面上滑行的总距离
知识点
如图所示,光滑曲面AB与水平面BC平滑连接于B点,BC右端连接内壁光滑、半径为r=0.4m的四分之一细圆管CD,管口D端正下方直立一根劲度系数为k=25N/m的轻弹簧,轻弹簧下端固定,上端恰好与管口D端齐平。质量为m=l kg的小球在曲面上距BC的高度为h=0.8m处从静止开始下滑,进入管口C端时与管壁间恰好无作用力,通过CD后压缩弹簧。已知弹簧的弹性势能表达式为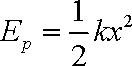
(1)小球达到B点时的速度大小vB;
(2)水平面BC的长度s;
(3)在压缩弹簧过程中小球的最大速度vm。
正确答案
(1)vB=4m/s
(2)s=1.2m
(3)vm=4m/s
解析
(1)由机械能守恒得:
解得:vB=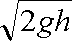
(2)由mg=m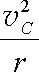
得vC=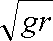
由动能定理得:
解得:s=1.2m
(3)设在压缩弹簧过程中小球速度最大时离D端的距离为x,则有:
kx=mg
得:x=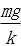
由功能关系得: mg(r+x)-


解得: vm=4m/s
知识点
如图所

正确答案
解析
略
知识点
扫码查看完整答案与解析