- 牛顿运动定律的综合应用
- 共404题
如图所示,足够长的斜面倾角θ=30°,斜面底端A点与一半径为R的光滑半圆轨道平滑连接,半圆轨道的直径与地面垂直。已知小物体与斜面间的动摩擦因数为μ=
(1)若小物体在斜面上从与圆心O等高的位置由静止释放,则小物体第一次滑到A点所用的时间为多少?
(2)在(1)的情况下,小物体在斜面上滑行的总路程为多少?
(3)要使小物体能通过圆轨道最高点B,求小物体在斜面上由静止释放的高度。
正确答案
(1)
(2)4R
(3)2.5R
解析
(1)物块沿斜面下滑过程中,在重力、支持力和摩擦力作用下做匀加速运动,设下滑加速度为a,到达斜面底端B时的时间为t,则:
mgsinθ﹣μmgcosθ=ma
则得:a=g(sinθ﹣μcosθ)=10×(sin30°﹣
物体的位移:
由
得:t=
(2)由题意可知,最后物块的机械能全部转化为内能,由功能关系得:μmgcosθS=mgR
整理得:S=4R
(3)要使小物体能通过圆轨道最高点B,在物体在最高点的向心力要大于等于重力,即:
从释放到到达B的过程中,由机械能守恒得:
联立以上方程得:h=2.5R
知识点
24.如图13所示,在某项娱乐活动中,要求质量为m的物体轻放到水平传送带上,当物体离开水平传送带后恰好落到斜面的顶端,且此时速度沿斜面向下.斜面长度为l=2.75m,倾角为θ=37°,斜面动摩擦因数μ1=0.5.传送带距地面高度为h=2.1 m,传送带的长度为L=3m,传送带表面的动摩擦因数μ2=0.4,传送带一直以速度v传=4m/s逆时针运动,g=10 m/s2,sin37°=0.6,cos37°=0.8
求:
(1)物体落到斜面顶端时的速度大小;
(2)物体从斜面的顶端运动到底端的时间;
(3)物体轻放在水平传送带的初位置到传送带左端的距离应该满足的条件.
正确答案
见解析。
解析
(1)物体离开传送带后做平抛运动,设落到斜面顶端的速度为v0,沿斜面方向vy=
vx=vycot θ=4m/s
v0=
(2)设物体从斜面的顶端运动到底端的时间为t,根据牛顿第二定律
mgsin θ-μ1mgcos θ=ma1
解得t=0.5 s
(3)设物体轻放在水平传送带的位置到传送带左端的距离为x,因为vx=v传
μ2mg=ma2
由
得x0=
物体轻放在水平传送带的初位置到传送带左端的距离范围为2 m≤x≤3 m
知识点
在光滑水平面上,A、B两小球沿水平面相向运动.当小球间距小于或等于L时,受到大小相等,方向相反的相互排斥恒力作用,当小球间距大于L时,相互间的排斥力为零,小球在相互作用区间运动时始终未接触,两小球的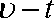
正确答案
解析
略。
知识点
如图所示,一辆载重卡车沿平直公路行驶,车上载有质量均为m的A、B两块长方体水泥预制件。己知预制件左端与车厢前挡板的距离为L,A、B间以及B与车厢间的动摩擦因数分别为
(1)卡车制动的加速度满足什么关系时,预制件A相对B滑动,而B相对车厢底板静止?
(2)卡车制动后为保证司机安全,在B相对车厢底板静止的情况下,预制件A不与车厢前挡板碰撞,则卡车从开始制动到停止所经历的时间应满足什么条件?
正确答案
(1)
(2)t
解析
(1)若A相对B滑动,则有:
即:
若B相对车厢底板滑动,则有:
即:
要使A相对B滑动,需满足
要使B相对于车厢底板静止,需满足
联立以上各式得:
(2)卡车制动后,设A的位移为s1,有
卡车的位移为s车,有:
要使A不与车厢的前挡板相碰,应满足
即
故:
设卡车制动时间为t,则有
得
知识点
31.如图。质量m=2kg的物体静止于水平地面的A处,A、B间距L=20m.用大小为30N,沿水平方向的外力拉此物体,经t0=2s拉至B处。(已知cos37°=0.8,sin37°=0.6.取g=10m/s2。)
(1)求物体与地面间的动摩擦因数μ;
(2)用大小为30N,与水平方向成37°的力斜向上拉此物体,使物体从A处由静止开始运动并能到达B处,求该力作用的最短时问t。
正确答案
(1)0.5
(2)1.03s
解析
(1)物体做匀加速运动
∴
由牛顿第二定律
∴
(2)设





∴
由于匀加速阶段的末速度即为匀减速阶段的初速度,因此有
∴
∴
(2)另解:设力
∴
由牛顿定律
∴
∵
知识点
7.滑雪运动中当滑板压地时会把雪内的空气逼出来,在滑雪板与雪地之间形成一个暂时的“气垫”,从而会影响滑雪板与雪地之间摩擦。当滑雪者的速度小于4m/s时滑雪板与地面之间的动摩擦因数为μ1=0.25;速度大于等于4m/s时,动摩擦因数为μ2=0.125一滑雪者从坡顶A处由静止开始自由滑下,滑至坡底B后再滑上一段水平雪地.已知LAB=20m,


(1)滑雪者从静止开始到第一次动摩擦因数发生变化所用时间;
(2)滑雪者滑至坡底B处时速度的大小。
正确答案
见解析
解析
(1)设滑雪者质量为m,滑雪者在斜坡上从静止开始加速至速度

解得:
故由静止开始到动摩擦因数发生变化所经历的时间:
(2)则根据牛顿定律和运动学公式有:



代入数据解得:
知识点
静止在光滑水平面上的物体,受到一个大小不为零的水平拉力作用,若拉力开始作用瞬间物体的速度大小为v,加速度大小为a,则下列判断中正确的是( )
正确答案
解析
略
知识点
把一重为G的物体用一个水平推力F=kt(k为恒量,t为时间)压在竖直且足够高的平整的墙上,如图所示,若物体和竖直墙壁间的动摩擦因数为μ,则从t =0开始( )
正确答案
解析
略
知识点
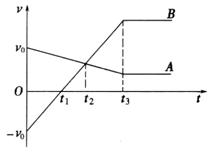
19.受水平外力F作用的物体,在粗糙水平面上作直线运动,其v-t 图线如图所示,则
正确答案
解析
略。
知识点
如图所示,某三角支架ABO中,轻杆BO可绕通过O点的光滑轴转动,B端固定一质量为m的小球, A、B间用细绳连接,调节细绳长度,使AO⊥OB,且绳与轻杆间夹角为37°。用外力保持杆AO竖直,使整个装置沿水平方向做直线运动。已知重力加速度为g,sin37°=0.6,cos37°=0.8。求:
(1)当整个装置做匀速直线运动时,细绳AB、轻杆OB对小球的作用力分别为多大?
(2)当整个装置沿水平方向以大小为a=
正确答案
见解析
解析
(1)FAB=

(2)若a向左,FAB=1.67mg,
由ma = FAB cos37°- FOB,可解得FOB= FAB cos37°- ma=1.33mg-0.33 mg= mg
若a向右,FAB=1.67mg
由ma = FOB- FAB cos37°可解得FOB= FAB cos37°+ ma=1.33mg+0.33 mg=1.67 mg
知识点
扫码查看完整答案与解析