- 牛顿运动定律的综合应用
- 共404题
如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”型导轨,在“U”型导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示。在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g=10m/s2)。
(1)通过计算分析4s内导体棒的运动情况;
(2)计算4s内回路中电流的大小,并判断电流方向;
(3)计算4s内回路产生的焦耳热。
正确答案
见解析。
解析
(1)导体棒先在无磁场区域做匀减速运动,有
代入数据解得:
导体棒在1s末已经停止运动,以后一直保持静止,离左端位置仍为
(2)前2s磁通量不变,回路电动势和电流分别为
后2s回路产生的电动势为
回路的总长度为
电流为
根据楞次定律,在回路中的电流方向是顺时针方向。
(3)前2s电流为零,后2s有恒定电流,焦耳热为
知识点
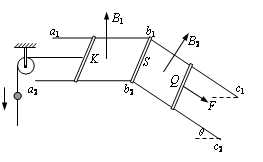
如图所示,间距l=0.3m的平行金属导轨a1b1c1和a2b2c2分别固定在两个竖直面内,在水平面a1b1b2a2区域内和倾角θ=37º的斜面c1b1b2c2区域内分别有磁感应强度B1=0.4T、方向竖直向上和B2=1T、方向垂直于斜面向上的匀强磁场。电阻R=0.3Ω、质量m1=0.1kg、长为l 的相同导体杆K、S、Q分别放置在导轨上,S杆的两端固定在b1、b2点,K、Q杆可沿导轨无摩擦滑动且始终接触良好。一端系于K杆中点的轻绳平行于导轨绕过轻质滑轮自然下垂,绳上穿有质量m2=0.05kg的小环。已知小环以a=6m/s2的加速度沿绳下滑,K杆保持静止,Q杆在垂直于杆且沿斜面向下的拉力F作用下匀速运动。不计导轨电阻和滑轮摩擦,绳不可伸长。取g=10 m/s2,sin37º=0.6,cos37º=0.8。求:
(1)小环所受摩擦力的大小;
(2)Q杆所受拉力的瞬时功率。
正确答案
见解析。
解析
(1)设小环受到摩擦力大小为f,则由牛顿第二定律得到
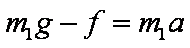
代入数据得到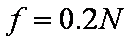
说明:①式3分,②式1分
(2)设经过K杆的电流为I1,由K杆受力平衡得到

设回路总电流为I,总电阻为R总,有

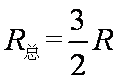
设Q杆下滑速度大小为v,产生的感应电动势为E,有
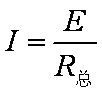
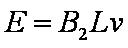
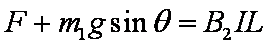
拉力的瞬时功率为P=Fv........⑨
联立以上方程得到P=2W......⑩
知识点
如图,将质量m=0.1kg的圆环套在固定的水平直杆上。环的直径略大于杆的截面直径。环与杆间动摩擦因数μ=0.8。对环施加一位于竖直平面内斜向上,与杆夹角θ=53°的拉力F,使圆环以a=4.4m/s2的加速度沿杆运劝,求F的大小。
正确答案
见解析。
解析
令
当
由牛顿定律
解得
当
由牛顿定律
解得

知识点
如图所示,水平板上有质量m=1.0kg的物块,受到随时间t变化的水平拉力F作用,用力传感器测出相应时刻物块所受摩擦力Ff的大小。取重力加速度g=10m/s2。下列判断正确的是
正确答案
解析
由图可得,物体与地面间的最大静摩擦力为4N,物体从第4秒开始运动,在第4秒-第5秒内发生位移,因此做功不为零;4秒末物块所受合力为0,N;4秒以后,物块所受摩擦力为滑动摩擦力,根据滑动摩擦力公式可求得动摩擦因数为0.3;根据牛顿第二定律可求得加速度为2.0m/s2。此题考查学生对基本的物理情景的分析。
知识点
某兴趣小组用如题25图所示的装置进行实验研究。他们在水平桌面I固定一内径为d的圆柱形玻璃杯,杯口I放置一直径为d ,质量为m 的均匀薄圆板,板内放一质量为2m的物块。板中心,物块均在杯的轴线,则物体与板间动摩擦因数为c,不考虑板与杯口之间的摩擦力,重力加速度为g,不考虑板翻转。
(1)对板施加指向圆心的水平外力F,设物块与板间最大静摩擦力为L,若物块能在板上滑动. 求F应满足的条件
(2)如果对板施加的指向圆心的水平外力是作用时间极短的较大冲击力,冲量为I
① I应满足什么条件才能使物块从板上掉下?
② 物块从开始运动到掉下时的位移s为多少?
③ 根据s与L的关系式,说明要使s更小,冲量应如何改变
正确答案
见解析
解析
解:
(1)设圆板与物块相对静止时,它们之间的静摩擦力为f,共同加速度为a
由牛顿运动定律,有
对物块 f=2ma 对圆板 F-f=ma
两物相对静止,有 f≤fmax
得 F≤
相对滑动的条件 F>
(2)设冲击刚结束时圆板获得的速度大小为v0,物块掉下时,圆板和物块速度大小分别为v1和v2.
由动量定理,有 I=mv0
由动能定理,有
对圆板-2



对物块2

由动量守恒定律,有
mv0=mv1+2mv2
要使物块落下,必须 v1>v2
由以上各式得
I>
s=
分子有理化得
s=
根据上式结果知:I越大,s越小.
知识点
扫码查看完整答案与解析