- 牛顿运动定律的综合应用
- 共404题
如图，竖直平面内的轨道I和II都由两段细直杆连接而成，两轨道长度相等。用相同的水平恒力将穿在轨道最低点B的静止小球，分别沿I和II推至最高点A，所需时间分别为t1、t2;动能增量分别为△Ek1、△Ek2,假定球在经过轨道转折点前后速度大小不变，且球与I. II轨道间的动摩擦因数相等，则
A△Ek1
B△Ek1=△Ek2 t1
C△Ek1
D△Ek1=△Ek2 t1
正确答案
解析
小球从最低点到最高点受到摩擦力做功：Wf＝μmgcosα×L＝μmgx水平与斜面倾角无关；水平拉力为恒力，水平位移相同，所以拉力做功相等，根据动能定理可知，两球到达A点时的速度相同，动能相等，AC项错误；将小球的运动看做直线运动，画出其速率随时间变化的图象，
可知，沿II轨道运动的小球先到达，B项正确。
知识点
如图所示，生产车间有两个相互垂直且等高的水平传送带甲和乙，甲的速度为v0。小工件离开甲前与甲的速度相同，并平稳地传到乙上，工件与乙之间的动摩擦因数为μ。 乙的宽度足够大，重力加速度为g。
(1)若乙的速度为v0，求工件在乙上侧向(垂直于乙的运动方向)滑过的距离s；
(2)若乙的速度为2v0，求工件在乙上刚停止侧向滑动时的速度大小v；
(3)保持乙的速度2v0不变，当工件在乙上刚停止滑动时, 下一只工件恰好传到乙上，如此反复。若每个工件的质量均为m，除工件与传送带之间摩擦外，其他能量损耗均不计，求驱动乙的电动机的平均输出功率P。
正确答案
答案：（1）
解析
（1）摩擦力与侧向的夹角为45°
侧向加速度大小
解得
（2）设t=0时刻摩擦力与侧向的夹角为
则
很小的
解得
且由题意可知
所以摩擦力方向保持不变
则当
即
（3）工件在乙上滑动的侧向位移为x，沿乙方向的位移为y
由题意知
在侧向上
工件滑动时间
工件相对乙的位移
则系统摩擦生热
电动机做功
由
知识点
如右图，轻弹簧上端与一质量为m的木块1相连，下端与另一质量为M的木块2相连，整个系统置于水平放置的光滑木板上，并处于静止状态。现将木板沿水平方向突然抽出，设抽出后的瞬间，木块1、2的加速度大小分别为
A
B
C
D
正确答案
解析
在抽出木板的瞬时，弹簧对1的支持力和对2的压力并未改变。对1物体受重力和支持力，mg=F,a1=0. 对2物体受重力和压力，根据牛顿第二定律
知识点
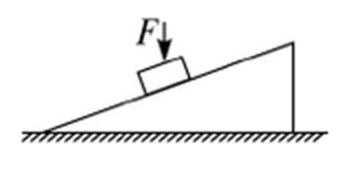
如图所示，放在固定斜面上的物块以加速度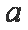
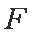
A物块可能匀速下滑
B物块仍以加速度
C物块将以大于
D物块将以小于
正确答案
解析
根据题意，放在斜面上的物块沿斜面以加速度a匀加速下滑，在沿斜面方向对物块由牛顿第二定律有mgsinθ－μmgcosθ＝ma①，在物块上施加竖直向下的力F后，在沿斜面方向对物块由牛顿第二定律有（mg＋F）sinθ－μ（mg＋F）cosθ＝ma0②，由①②易知a0＞a，C项正确、A、B、D三项错误。
知识点
如图，水平地面上的矩形箱子内有一倾角为
(1)求箱子加速阶段的加速度大小a'。
(2)若a>g tan
正确答案
（1）
解析
（1）设加速过程中加速度为a‘，由匀变速运动公式
解得
（2）设球不受车厢作用，应满足
解得
减速时加速度由斜面支持力N与左壁支持力P共同决定，当
P＝0
球受力如图。
由牛顿定律
解得
知识点
扫码查看完整答案与解析