- 函数的图象与图象变化
- 共172题
13.设a>0,b>0. 若关于x,y的方程组

正确答案
知识点
3.已知平行直线



正确答案
解析
利用平行线间距离公式得:
考查方向
解题思路
平行线间距离公式;也可以转化为点到直线距离公式
易错点
用错公式
知识点
8.定义区间[x1,x2]的长度为x2-x1,已知函数f(x)=3|x|的定义域为[a,b],值域为[1,9],则区间[a,b]的长度的最大值为______,最小值为______.
正确答案
4;2
解析
由3|x|=1得x=0,由3|x|=9得x=±2
故满足题意的定义域可以为[-2,m](0≤m≤2)或[n,2](-2≤n≤0)
故区间[a,b]的长度的最大值为4,最小值为2.
知识点
11.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲,乙,丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是 ( )
正确答案
解析
“燃油效率”是指汽车每消耗1升汽油行驶的里程,A中乙车消耗1升汽油,最多行驶的路程为乙车图象最高点的纵坐标值,A错误;B中以相同速度行驶相同路程,甲燃油效率最高,所以甲最省油,B错误,C中甲车以80千米/小时的速度行驶1小时,甲车每消耗1升汽油行驶的里程10km,行驶80km,消耗8升汽油,C错误,D中某城市机动车最高限速80千米/小时. 由于丙比乙的燃油效率高,相同条件下,在该市用丙车比用乙车更省油,选D
考查方向
.函数应用问题;对“燃油效率”新定义的理解;对图象的理解。
解题思路
根据新定义的概念,做出图象求解
易错点
不理解新定义的概念,对函数图象理解不透彻
知识点
7. 定义






正确答案
解析
根据矩阵的定义,可以得到
所以
所以图象向右平移可得,
所以选A
考查方向
解题思路
先根据矩阵的定义,得到f(x)的解析式,然后根据函数的解析式平移可得
易错点
三角函数公式记忆混淆
知识点
2.欧拉公式


正确答案
解析




考查方向
解题思路
先写出

易错点
不理解题目中的背景而出现失误,另外对于
知识点
9. 设函数





正确答案
解析
根据在x=-2处取得极小值,则在x<-2时导数小于0,x>-2时导数大于0,等于-2时导数值等于0,所以在小于0的部分图像应该满足在x<-2在x轴上方,-2
考查方向
解题思路
根据在x=-2处取得极小值,则在x<-2时导数小于0,x>-2时导数大于0,等于-2时导数值等于0,然后导函数与x相乘之后可以根据正负找到正确的图像。
易错点
抽象函数没有具体解析式无法下手。
知识点
9.已知直线



正确答案

解析
根据两条直线的平行关系,可得到

考查方向
本题考查了平面几中的直线位置关系,是高考常考题型之一。
解题思路
利用直线平行的条件,直线间的距离公式即可直接解答。
易错点
常与直线垂直的条件混淆,利用平行线间的距离公式要注意系数对应相等。
知识点
11.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲,乙,丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是 ( )
正确答案
解析
“燃油效率”是指汽车每消耗1升汽油行驶的里程,A中乙车消耗1升汽油,最多行驶的路程为乙车图象最高点的纵坐标值,A错误;
B中以相同速度行驶相同路程,甲燃油效率最高,所以甲最省油,B错误,
C中甲车以80千米/小时的速度行驶1小时,甲车每消耗1升汽油行驶的里程10km,行驶80km,消耗8升汽油,C错误,
D中某城市机动车最高限速80千米/小时. 由于丙比乙的燃油效率高,相同条件下,在该市用丙车比用乙车更省油,选D.
考查方向
函数应用问题;对“燃油效率”新定义的理解;对图象的理解。
解题思路
根据新定义的概念,做出图象求解
易错点
不理解新定义的概念,对函数图象理解不透彻
知识点
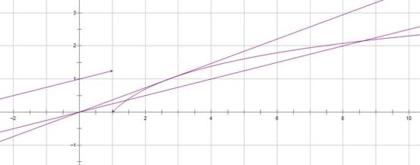
13.已知函数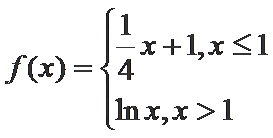
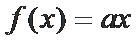
取值范围是___________
正确答案
解析
∵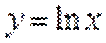
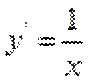
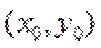
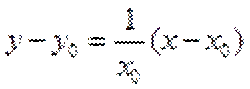
∴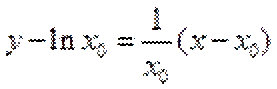
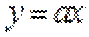
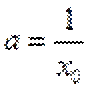
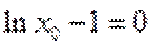
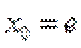
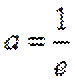
当直线与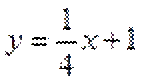
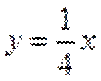
当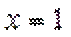
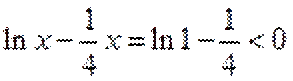
当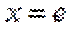
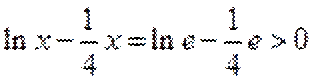
当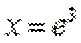
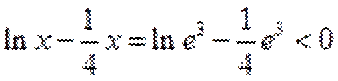
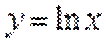
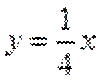
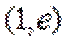
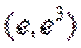
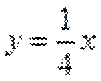
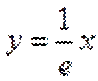
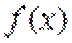
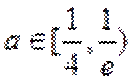
考查方向
解题思路
本题考查运用导数解决函数的能力,解题步骤如下: 先求导,找函数的切线方程,再利用零点的判定方法,找到a的取值范围。
易错点
本题必须注意审题,忽视则会出现错误。
知识点
扫码查看完整答案与解析