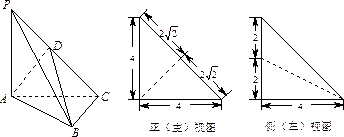- 直线与平面垂直的判定与性质
- 共118题
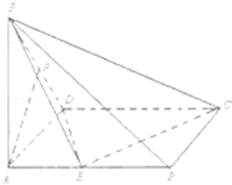
已知在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,PA=AD=1,E,F分别是AB、PD的中点。
(1)求证:AF⊥平面PDC;
(2)求三棱锥B﹣PEC的体积;
(3)求证:AF∥平面PEC。
正确答案
见解析。
解析
(1)证明:∵PA⊥平面ABCD,∴PA⊥CD,
由底面ABCD是矩形,∴CD⊥DA,又PA∩AD=A,∴CD⊥平面PAD,
∴CD⊥AF。
∵PA=AD=1,F是PD的中点,
∴AF⊥PD,
又PD∩DC=D,∴AF⊥平面PDC。
(2)解: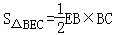
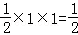
∵PA⊥平面ABCD,
VB﹣PEC=VP﹣BEC=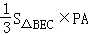

(3)
取PC得中点M,连接MF、ME。
∵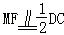
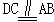
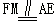
∴四边形AEMF是平行四边形,
∴AF∥EM。
又AF⊄平面PEC,EM⊂平面PEC,
∴AF∥平面PEC。
知识点
如图,已知平面












正确答案
解析
因为



设



在三角形中有





知识点
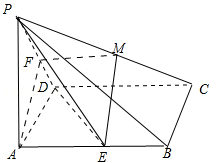
如图,矩形ABCD中,对角线AC、BD的交点为G,AD⊥平面ABE,AE⊥EB,AE=EB=BC=2,F为CE上的点,且BF⊥CE。
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-GBF的体积。
正确答案
见解析。
解析
知识点
如图,在三棱锥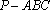
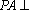
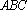
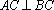
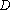
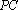
(1)证明: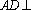
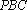
(2)求三棱锥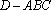
(3)在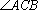
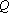
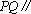
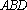
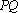
正确答案
见解析。
解析
(1)因为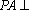
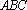
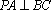
又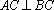
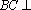
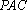
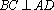
由三视图可得,在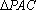
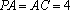
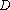
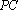
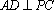
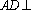
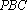
(2)由三视图可得
由⑴知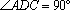

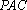
又三棱锥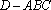
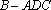
所以,所求三棱锥的体积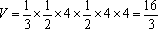
(3)取


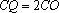
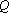
因为
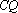
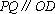
因为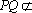
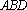
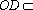

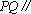
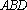
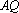
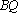

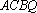
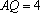
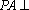
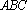
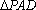
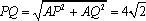
知识点
设




①若






③若






其中,正确命题的个数是
正确答案
解析
略
知识点
扫码查看完整答案与解析