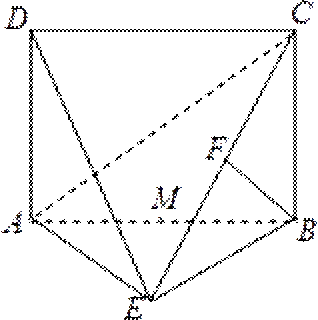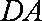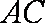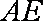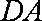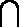- 直线与平面垂直的判定与性质
- 共118题
如图所示,平面





(1)求证:

(2)求三棱锥
正确答案
见解析。
解析
(1)
证明:

又∵ABCD为正方形,∴BC//AD,∴BC//EF。 …………4分
又

(2)∵平面PAD⊥平面ABCD,CD⊥AD,∴CD⊥平面PAD,即GD⊥平面AEF。 ……8分
又∵EF//AD,PA⊥AD,∴EF⊥AE。 …………10分
又

知识点
如图,四边形


(1) 求证:
(2) 求证:平面
(3) 求体积

正确答案
见解析。
解析
(1)
设BD交AC于M,连结ME.
∵ABCD为正方形,所以M为AC中点,
又∵E为

∴
∴
(2)∵ABCD为正方形 ∴
∵
又
∵
∴
(3)
知识点
如图,四棱锥P—ABCD中,PD⊥平面ABCD,底面ABCD为矩形,PD=DC=4,AD=2,E为PC的中点.
(1)求证:AD⊥PC;
(2)求三棱锥P-ADE的体积;
(3)在线段AC上是否存在一点M,使得PA//平面EDM,若存在,求出AM的长;若不存在,请说明理由.
正确答案
见解析。
解析
(1)证明:因为PD⊥平面ABCD.
所以PD⊥AD.
又因为ABCD是矩形,
所以AD⊥CD.…………………………………………………………………2分
因为
所以AD⊥平面PCD.
又因为
所以AD⊥PC.………………………………4分
(2)解:因为AD⊥平面PCD,VP-ADE=VA-PDE,…………………………………6分
所以AD是三棱锥A—PDE的高.
因为E为PC的中点,且PD=DC=4,
所以
又AD=2,
所以
(3)
取AC中点M,连结EM、DM,
因为E为PC的中点,M是AC的中点,
所以EM//PA,
又因为EM

所以PA//平面EDM.…………………………………………………………10分
所以
即在AC边上存在一点M,使得PA//平面EDM,AM的长为
知识点
如图,四边形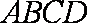
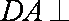
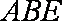
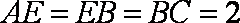
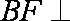
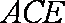
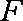
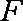
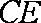
(1)求证:
(2)求四棱锥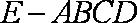
(3)设点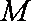
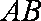
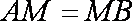
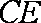
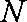
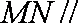
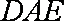
正确答案
见解析。
解析
(1)因为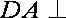
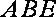
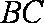
所以
因为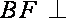
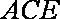
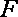

因为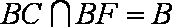
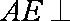
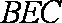
则
因为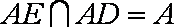
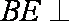
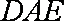
则

(2)
作

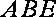
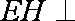
因为
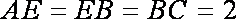
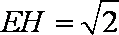

(3)因为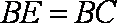
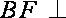
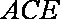
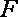
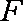
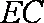
设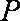
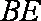
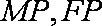
所以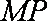
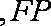
因为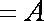
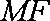
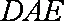
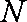
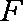
知识点
如图,三棱柱ABC—A′B′C′=1,BC=1,BC′=1,CC′=
(1)求证;EF//平面A′B′C′;
(2)求证:平面ABC′⊥平面A′B′C′。
正确答案
见解析。
解析
(1)证明:取


又
(2)













知识点
扫码查看完整答案与解析