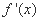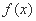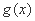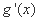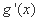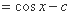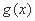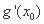- 函数性质的综合应用
- 共80题
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:简答题
|
已知函数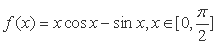
(1)求证: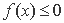
(2)若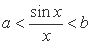
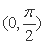
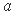
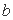
正确答案
见解析。
解析
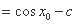
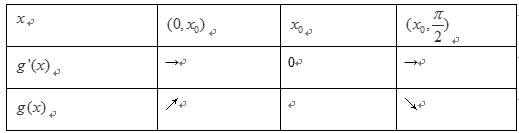
(1)由

因为在区间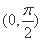
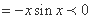
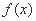
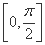
从而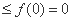
(2)当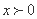
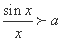
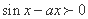
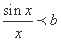
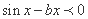
令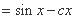
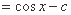
当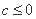
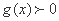
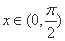
当
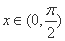
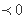
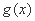
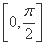
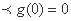
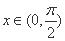
当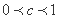
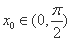
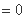
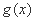
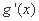
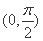
因为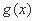
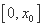
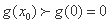

任意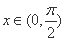
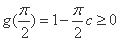
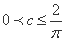
综上所述,当且仅当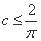
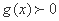
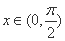
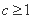
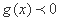
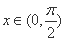
所以,若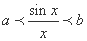
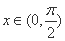

知识点
函数的最值及其几何意义函数性质的综合应用
1
题型:简答题
|
已知











(1)当


(2)设












正确答案
见解析。
解析
知识点
元素与集合关系的判断函数性质的综合应用
1
题型:
单选题
|
设函数












正确答案
C
解析
无论





即



画出这两个图象可以看出


知识点
函数性质的综合应用
下一知识点 : 函数的值
扫码查看完整答案与解析