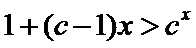- 函数性质的综合应用
- 共80题
设函数
25.讨论函数

26.记


27.在(Ⅱ)中,取


正确答案
(Ⅰ)极小值为
解析
(Ⅰ)



因为

①当

②当

③当







因此,




考查方向
解题思路
(Ⅰ)将



求导得





















易错点
函数求导错误,分类讨论能力弱,计算能力弱
正确答案
解析
:
(Ⅱ)

当

当

由此可知,函数


考查方向
解题思路
当




易错点
绝对值不等式性质运用错误,计算错误,不会合理放缩不等式
正确答案
(Ⅲ)1.
解析
(Ⅲ)



取


由此可知,

考查方向
解题思路
(Ⅲ)当








易错点
平均值不等式的性质,计算能力弱
5. 已知点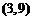
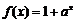

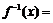
正确答案
解析
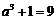
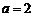
∴
∴
知识点
7. 方程

正确答案
解析

∴
∴
∴
知识点
设函数





24.求




25.设



正确答案
(Ⅰ)




又由基本不等式,有
解析
(Ⅰ)由



联立①②解得

当



又由基本不等式,有

考查方向
解题思路
(Ⅰ)将等式










易错点
导函数计算出错。
正确答案
(Ⅱ)由(Ⅰ)得


当




















解析
(Ⅱ)由(Ⅰ)得 

当




设函数 
当













考查方向
解题思路
(Ⅱ)由(Ⅰ)得






易错点
计算量大。
设函数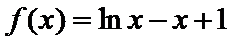
25.讨论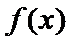
26.证明当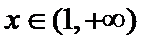
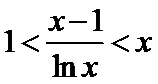
27.设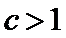
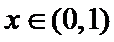
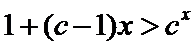
正确答案
(Ⅰ)当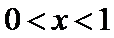
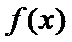
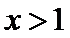
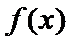
解析
(I)由题设,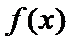
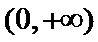
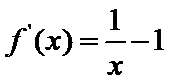
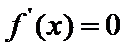
当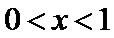
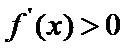
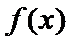
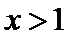
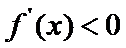
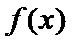
考查方向
解题思路
(I)首先求出导函数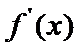
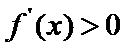
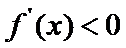
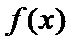
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅱ)(II)由(I)知,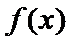
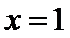
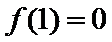
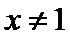
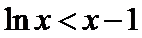
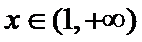
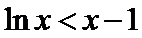
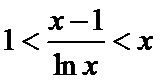
解析
(II)由(I)知,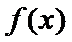
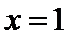
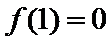
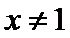
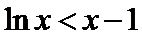
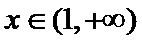
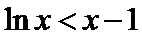
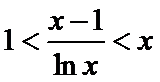
考查方向
解题思路
(II)左端等式可利用(I)的结论证明,右端将左端的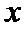

易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅲ)(III)由题设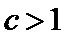
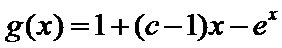
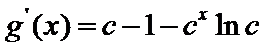
解得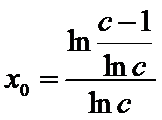
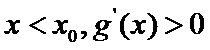
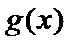
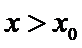
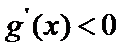
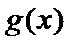
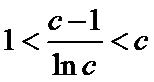
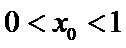
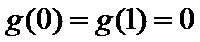
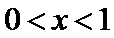
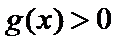
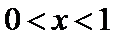
解析
(III)由题设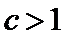
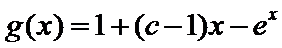
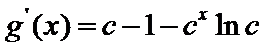
解得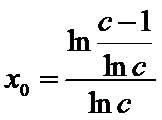
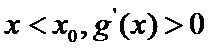
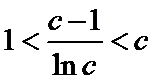
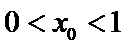
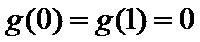
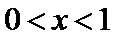
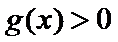
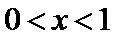
考查方向
解题思路
变形所证不等式构造新函数,然后通过利用导数研究函数的单调性来处理
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
扫码查看完整答案与解析