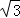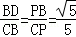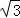- 直线的倾斜角与斜率
- 共278题
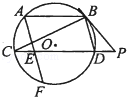
如图,⊙O的直径AB的延长线与弦CD的延长线相
交于点P,E为⊙O上一点,AE=AC, DE交AB于
点F。求证:△PDF∽△POC。
正确答案
见解析。
解析
因AE=AC,AB为直径,
故∠OAC=∠OAE,
所以∠POC=∠OAC+∠OCA=∠OAC+∠OAC=∠EAC。
又∠EAC=∠PDE,
所以,∠PDE=∠POC。
知识点
已知直线






正确答案
解析
因为







知识点
如图,AB、CD是圆O的两条平行弦,AF∥BD交CD于点E,交圆为O于点F,过B点的切线交CD的延长线于点P,若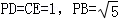
正确答案
解析
∵直线PB切圆O于点B,PDC是圆O的割线
∴PB2=PD×PC,得(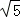
解得CD=4,得PC=5,ED=CD﹣CE=3
∵∠PBD=∠PCB,∠BPD=∠CPB
∴△BPD∽△CPB,可得
设BD=x,则CB=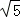
∵AE∥BD,得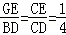
∴GE=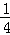
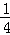
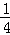
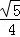
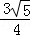
平等四边形ABDE中,AE=BD=x,得AG=AE﹣GE=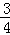
由相交弦定理,得AG•GF=CG•BG,即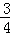
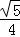
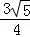
解得GF=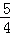
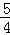
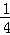
又∵AE•EF=CE•ED,AE=EF=x,CE=1且ED=3
∴x2=1×3=3,解之得x=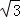
故答案为:
知识点
已知直线l的参数方程为
正确答案

解析
解:直线l的普通方程为4x﹣3y+3m=0,圆C的直角坐标方程为x2+y2﹣2x=0。
所以圆心C(1,0)到直线l的距离d=
解得m=
故答案为:
知识点
若直线


正确答案
解析
圆方程化为:(x-1)2+(y-1)2=4,圆心坐标为(1,1),因为直线平分圆,所以它必过圆心,因此,有:a+b=1,





知识点
扫码查看完整答案与解析