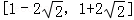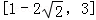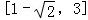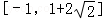- 直线的倾斜角与斜率
- 共278题
若设变量x,y满足约束条件

正确答案
解析
知识点
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC。
(1)求证:AC⊥平面BDEF;
(2)求证:FC∥平面EAD;
(3)求二面角A﹣FC﹣B的余弦值。
正确答案
见解析。
解析
(1)连接FO,因为四边形ABCD为菱形,所以AC⊥BD,且O为AC中点,
又 FA=FC,所以 AC⊥FO,
因为 FO∩BD=O,
所以 AC⊥平面BDEF,
(2)因为四边形ABCD与BDEF均为菱形,
所以AD∥BC,DE∥BF,
所以 平面FBC∥平面EAD,
又FC⊂平面FBC,所以FC∥平面EAD,
(3)因为四边形BDEF为菱形,且∠DBF=60°,
所以△DBF为等边三角形。
因为O为BD中点,所以FO⊥BD,故FO⊥平面ABCD。
由OA,OB,OF两两垂直,建立如图所示的空间直角坐标系O﹣xyz,
设AB=2.因为四边形ABCD为菱形,∠DAB=60°,
则BD=2,所以OB=1,

所以 

设平面BFC的法向量为
则有
取x=1,得
∵平面AFC的法向量为
由二面角A﹣FC﹣B是锐角,得|cos<



所以二面角A﹣FC﹣B的余弦值为
知识点
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足cos

(1) 求△ABC的面积;
(2) 若c=1,求a、sinB的值。
正确答案
见解析。
解析
(1) cosA=2×

而

又A∈(0,π),∴sinA=
∴S=


(2) ∵bc=5,而c=1,∴b=5.…………………………………………………8分
∴

又

知识点
如图,已知AB和AC是圆的两条弦.过点B作圆的切线与AC的延长线相交于点D,过点C作BD的平行线与圆相交于点E,与AB相交于点F,



正确答案
解析
∵













知识点
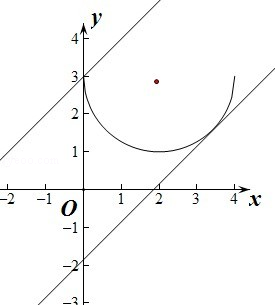
若直线y=x+m与曲线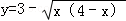
正确答案
解析
由x(4﹣x)≥0,得0≤x≤4.由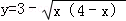
即(x﹣2)2+(y﹣3)2=4,因为0≤x≤4,所以曲线为圆心为(2,3),半径为2的下半圆。
圆心到直线距离d=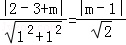
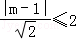
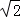
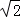
因为圆是下半圆,所以当直线y=x+m经过点(0,3)时,m取到最大值3,所以1﹣2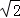
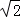
故选B,
知识点
在△ABC中,内角A、B、C的对边分别为a、b、c,已知a2+b2=6abcosC,且sin2c=2sinAsinB。
(1)求角C的大小;
(2)设函数f(x)=sin


正确答案
见解析。
解析
(1)因为a2+b2=6abcosC,由余弦定理知,a2+b2=c2+2abcosC,
所以,cosC=
所以,cosC=



(2)f(x)=sin





由已知,得:

因为C=


故根据正弦函数的图象,得:
知识点
如图,三棱柱




(1)求证:
(2)求二面角
(3)求点

正确答案
见解析
解析
(1)∵



∵ 

∴ 在直角


∵ 


∴ 在

∴


(2)取



∵ 

∵ 



∴ 

延长




∴ 四边形




∴ 四边形
∴ 在直角

(3)取




∵ 


∴ 

设点


∴
∴ 

解法二
(1)∵


取



∵ 




以


建立如图空间直角坐标系,则
∴
∵
∴ 

(2)

∵ 


∴
设平面

∴ 


∴ 

∴ 二面角

(3)设点




知识点
如图,在四棱锥P—ABCD中,底面ABCD为直角梯形,且AD//BC,



(1)求证:CD
(2)侧棱PA上是否存在点E,使得BE//平面PCD?若存在,指出点E的位置并证明,若不存在,请说明理由;
(3)求二面角A—PD—C的余弦值。
正确答案
见解析。
解析
解法一:
因为 
所以
又因为侧面

且侧面

所以 

又因为
所以


分别以





设





(1)


所以 



又因为


(2)在


证明如下:侧棱



设平面

因为

所以


所以

因为



(3)由已知,



由(2)知,

设二面角

即二面角

解法二:(1)因为 

又因为侧面



所以




在底面


所以 


又因为


(2)
在



证明如下:取

连结


则

由已知
所以

所以

所以四边形

因为



所以

(3)
取


则 
又因为平面

所以 

过


连结

所以

设


在


所以 

即二面角

知识点
如图,在四棱锥P—ABCD中,底面ABCD为直角梯形,且AD//BC,



(1)求证:CD
(2)侧棱PA上是否存在点E,使得BE//平面PCD?若存在,指出点E的位置并证明,若不存在,请说明理由;
(3)求二面角A—PD—C的余弦值。
正确答案
见解析
解析
解法一:
因为 
所以
又因为侧面

且侧面

所以 

又因为
所以


分别以





设





(1)


所以 



又因为


(2)在


证明如下:侧棱



设平面

因为

所以


所以

因为



(3)由已知,






设二面角

即二面角

解法二:(1)因为 

又因为侧面



所以




在底面


所以 


又因为


(2)
在



证明如下:取

连结


则

由已知
所以

所以

所以四边形

因为



所以

(3)
取


则 
又因为平面

所以 

过


连结

所以

设


在


所以 

即二面角

知识点
已知倾斜角为



正确答案
解析
依题意,得:




知识点
扫码查看完整答案与解析