- 圆锥曲线的定点、定值问题
- 共43题
1
题型:
单选题
|
已知双曲线




正确答案
C
解析
略
知识点
圆锥曲线的定点、定值问题圆锥曲线中的探索性问题
1
题型:简答题
|
已知抛物线和双曲线都经过点
(1)求抛物线和双曲线标准方程;
(2)已知动直线m过点P(3,0),交抛物线于A,B两点,记以线段AP为直径的圆为圆C,
求证:存在垂直于x轴的直线l被圆C截得的弦长为定值,并求出直线l的方程。
正确答案
见解析。
解析
知识点
双曲线的定义及标准方程抛物线的标准方程和几何性质直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题直线、圆及圆锥曲线的交汇问题
1
题型:简答题
|
设F为抛物线E: 

(1)求抛物线方程;
(2)设动直线l与抛物线E相切于点P,与直线
正确答案
见解析
解析
解析:(1)由



(2)设点P(




切线方程:y-

由

设M(0,










故以PQ为直径的圆过y轴上的定点M(0,1)
知识点
向量在几何中的应用抛物线的标准方程和几何性质直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题
1
题型:简答题
|
20.如图,设点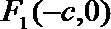
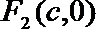
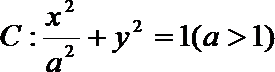
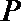
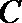

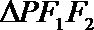
(1)求椭圆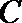
(2)设直线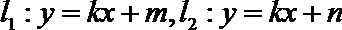
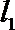
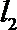
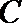
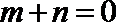
(3)在(2)的条件下,试探究在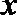
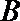

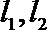
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题圆锥曲线中的探索性问题
1
题型:简答题
|
20.已知椭圆





(1)求椭圆C的方程;
(2)设椭圆










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题
下一知识点 : 圆锥曲线中的探索性问题
扫码查看完整答案与解析