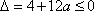- 变化的快慢与变化率
- 共66题
函数f(x)=ex+x2﹣2在区间(﹣2,1)内零点的个数为( )
正确答案
解析
解:∵f(x)=ex+x2﹣2
得f'(x)=ex+2x
f''(x)=ex+2>0
从而f'(x)是增函数,
f'(﹣2)=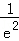
f'(0)=1>0
从而f'(x)在(﹣2,1)内有唯一零点x0,满足
则在区间(﹣2,x0)上,有f'(x)<0,f(x)是减函数,
在区间(x0,1)上,f'(x)>0,f(x)是增函数。
因为f(﹣2)=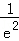
从而f(x)在(﹣2,1)上有两个零点。
故选B
知识点
已知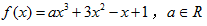
(1)当a=-3时,求证: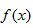
(2)如果对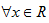
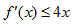
正确答案
见解析。
解析
(1)当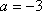

∵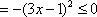
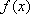
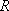
(2)∵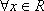
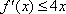
即
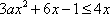
∴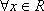
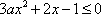
当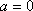
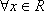
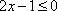
当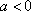
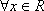
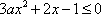
即
∴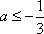
当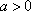
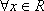
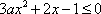
综上所述,
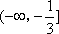
知识点
设二次函数f(x)=ax2﹣4x+c(x∈R)的值域为[0,+∞),则
正确答案
解析
解:由题意知,a>0,△=1﹣4ac=0,∴ac=4,c>0,
则 则


则
故选A。
知识点
设数列{an}满足an+1=2an+n2﹣4n+1。
(1)若a1=3,求证:存在f(n)=an2+bn+c(a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(2)若an是一个等差数列{bn}的前n项和,求首项a1的值与数列{bn}的通项公式。
正确答案
见解析。
解析
(1)∵数列{an}满足an+1=2an+n2﹣4n+1,
设an+1 +a(n+1)2+b(n+1)+c=2(an+an2+bn+c),即 an+1=2an+an2+(b﹣2a)n+c﹣a﹣b,
∴

∵a1+1﹣2=2,∴存在f(n)=n2﹣2n,使数列{an+f(n)}是等比数列,
∴an+n2﹣2n=2×2n﹣1,
∴an=2n﹣n2+2n。
(2)若an是一个等差数列{bn}的前n项和,数列{an}满足an+1=2an+n2﹣4n+1,
即an+1+(n+1)2﹣2(n+1)=2(an+n2﹣2n),
∴(an+n2﹣2n)=(a1﹣1)•2n﹣1,an=﹣n2+2n+(a1﹣1)•2n﹣1,
∴bn=
再根据{bn}是等差数列,∴a1=1,bn=﹣2n+3。
知识点
已知





正确答案
解析
解:∵

∴
又因为
所以
解得k=8,
故选C
知识点
设函数


正确答案
解析

知识点
等差数列


正确答案
解析
令首项为


知识点
已知实数


正确答案
解析
略
知识点
已知正数x,y满足x+2y=2,则
正确答案
9
解析
∵正数x,y满足x+2y=2,
∴



∴
知识点
已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样。
(1)若第五组抽出的号码为22,写出所有被抽出职工的号码;
(2)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的平均数;
(3)在(2)的条件下,从体重不轻于73公斤(
正确答案
(1)号码依次分别为:2,7,12,17,22,27,32,37,42,47(2)71(3)
解析
解析:(1)由题意,第5组抽出的号码为22.
因为2+5×(5-1)=22,所以第1组抽出的号码应该为2,抽出的10名职工的号码依次分别为:2,7,12,17,22,27,32,37,42,47. -------------------------- 4分
(2)这10名职工的平均体重为:=×(81+70+73+76+78+79+62+65+67+59)=71 ------------------------ 7分
(3)从这10名职工中随机抽取两名体重不轻于73公斤的职工,共有10种不同的取法:(73,76),(73,78),(73,79),(73,81),(76,78),(76,79),(76,81),(78,79),(78,81),(79,81),其中体重之和大于等于154公斤的有7种,故所求概率
知识点
扫码查看完整答案与解析