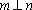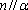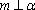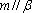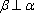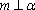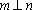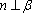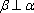- 直线与直线垂直的判定与性质
- 共82题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设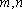
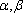
正确答案
解析
对A,若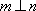
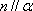

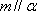
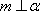
对B,若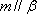
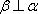

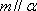

对C,若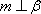
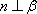
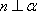
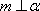
对D,若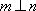
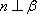
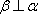
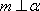

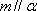
故选C. 点评:本题考查空间中的线线、线面、面面的闻之关系,容易题
知识点
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥平面ABCD,PA⊥AD.E和F分别是CD和PC的中点。
求证:
(1)PA⊥底面ABCD;
(2)BE∥平面PAD;
(3)平面BEF⊥平面PCD.
正确答案
见解析
解析
(1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,
所以PA⊥底面ABCD.
(2)因为AB∥CD,CD=2AB,E为CD的中点,
所以AB∥DE,且AB=DE.
所以ABED为平行四边形。
所以BE∥AD.
又因为BE

所以BE∥平面PAD.
(3)因为AB⊥AD,而且ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD,所以PA⊥CD.
所以CD⊥平面PAD.所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PD∥EF.所以CD⊥EF.
所以CD⊥平面BEF.
所以平面BEF⊥平面PCD.
知识点
如图,在正方体ABCD﹣A1B1C1D1中,E、F、P、Q、M、N分别是棱AB、AD、DD1、BB1、A1B1、A1D1的中点,求证:
(1)直线BC1∥平面EFPQ;
(2)直线AC1⊥平面PQMN。
正确答案
略。
解析
(1)在正方体ABCD﹣A1B1C1D1中,连接AD1,
∵AD1∥BC1,且F、P分别是AD、DD1的中点,
∴FP∥AD1,∴BC1∥FP,
又FP⊂平面EFPQ,且BC1⊄平面EFPQ,
∴直线BC1∥平面EFPQ;
(2)如图,
连接AC、BD,则AC⊥BD,∵CC1⊥平面ABCD,BD⊂平面ABCD,
∴CC1⊥BD;
又AC∩CC1=C,∴BD⊥平面ACC1,
又AC1⊂平面ACC1,∴BD⊥AC1;
又∵M、N分别是A1B1、A1D1的中点,
∴MN∥BD,∴MN⊥AC1;
同理可证PN⊥AC1,
又PN∩MN=N,∴直线AC1⊥平面PQMN。
知识点
如图,四棱锥



(1)求证:
(2)求证:
正确答案
;见解析。
解析
(1)连接AC交BE于点O,连接OF,不妨设AB=BC=1,则AD=2

又
(2)


知识点
如图,四棱锥



(1)证明:
(2)若


正确答案
见解析
解析
(1)证明:连接


又
而



(2) 由(1)

知识点
如图,四棱锥





(1)证明:
(2)求AB与平面SBC所成角的大小。
正确答案
见解析。
解析
解法一:(1)
取







又

所以
由








所以

另解:由已知易求得






(2)由



作



作


连结

又




作







由于






设




解法二:以



设


又设

(1)

由

故
由

又由

即

于是

故

所以

(2)设平面

则
又
故
取


故


知识点
已知点P,A,B,C,D是球O表面上的点,PA⊥平面ABCD,四边形ABCD是边长为

正确答案
解析
如图所示,∵PA⊥平面ABCD,
∴PA⊥AC。
故可知PC为球O直径,则PC的中点为O,取AC的中点为O′,
则
又∵

∴
∴球半径


∴△OAB为等边三角形。
∴
知识点
设m,n是两条不同的直线,α,β是两个不同的平面( )。
正确答案
解析
A选项中直线m,n可能平行,也可能相交或异面,直线m,n的关系是任意的;B选项中,α与β也可能相交,此时直线m平行于α,β的交线;D选项中,m也可能平行于β.故选C
知识点
如图,在四棱台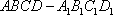
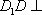
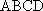
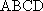
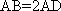
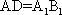
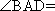
(1)证明: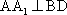
(2)证明: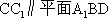
正确答案
见解析。
解析
(1)证明:因为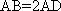
AD=a,则AB=2a,又因为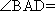
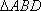
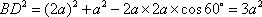
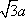

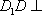
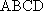


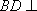
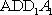
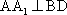
(2)连结AC,设AC
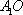
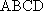
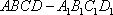
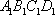
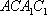
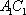
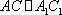
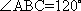
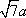
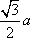
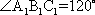
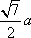


知识点
扫码查看完整答案与解析