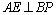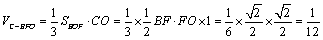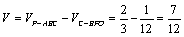- 直线与平面垂直的判定与性质
- 共118题
19.已知正方体



(1)求异面直线

(2)求四面体
正确答案
(1)由



连接


所以
即异面直线


(利用空间向量同样给分)
(2)算出




该四面体

解析
解析已在路上飞奔,马上就到!
知识点
如图,在四棱锥A—BCDE中,平面





(1)证明:

(2)求直线
正确答案
见解析
解析
证明:(1)连接



由

又平面


(2)在直角梯形


又平面


做








在


在


在


所以,直线

知识点
如图5,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,


(1)求证:OD//平面VBC;
(2)求证:AC⊥平面VOD;
(3)求棱锥
正确答案
见解析。
解析
(1)∵ O、D分别是AB和AC的中点,∴OD//BC .
又

(2)∵VA=VB,O为AB中点,∴
连接



∴


∵


∵

又∵



∵VO平面VOD,VD平面VOD,

(3)由(2)知


又∵点C是弧的中点,∴

∴三角形

∴棱锥

故棱锥

知识点
如图,已知





的中点。
(1)求证:

(2)求证:平面BCE⊥平面
(3)求此多面体的体积
正确答案
见解析。
解析
(1)取CE中点P,连结FP、BP,∵F为CD的中点, ∴FP∥DE,且FP=
又AB∥DE,且AB=
∴ABPF为平行四边形,∴AF∥BP,
又∵AF

(2)∵
∵AB⊥平面ACD,DE//A

∴DE⊥AF 又AF⊥CD,CD∩DE=D
∴AF⊥平面
又∵BP
(3)此多面体是一个以C为定点,以四边形ABED为底边的四棱锥,


知识点
各项均为正数的等比数列




正确答案
解析
略。
知识点
如图3,在四棱锥
(1)求证:BG平面PAD;
(2)求三棱锥G—CDP的体积;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF平面ABCD,并证明你的结论.
正确答案
见解析。
解析
证明:连结BD.
因为ABCD为棱形,且∠DAB=60°,所以ABD为正三角形.
又G为AD的中点,所以BG⊥AD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD.
(2)因为G为正三角形PAD的边AD的中点,所以PGAD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
所以PG⊥平面ABCD.
因为正三角形PAD的边长为2,所以
在CDG中,CD=2,DG=1,∠CDG=120°,
所以
故
(3)当F为PC的中点时,平面DEF⊥平面ABCD.
取PC的中点F,连结DE,EF,DF,CG,且DE与CG相交于H.
因为E、G分别为BC、AD的中点,所以四边形CDGE为平行四边形.
故H为CG的中点. 又F为CP的中点,所以FH//PG.
由(2),得PG平面ABCD,所以FH平面ABCD.
又FH平面DEF,所以平面DEF⊥平面ABCD.
知识点
如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点。
(1)证明:PB∥平面AEC;
(2)设AP=1,AD=

正确答案
见解析。
解析
(1)证明:设BD与AC 的交点为O,连结EO,∵ABCD是矩形,∴O为BD的中点
∵E为PD的中点,∴EO∥PB,EO⊂平面AEC,PB⊄平面AEC∴PB∥平面AEC;
(2)∵AP=1,AD=



∴AB=
又
知识点
如图,四棱锥



(1)求证:
(2)求异面直线

正确答案
见解析
解析
(1)∵

∴CD⊥SD
又四边形ABCD是正方形,∴CD⊥AD
∴CD⊥平面SDA

∴SA⊥CD.
(2)∵
∴


由(1),BA⊥平面SDA,∴△SAB是直角三角形.

故异面直线SB与CD所成角的大小为
知识点
如图,已知四棱锥



且
(1)求证:

(2)求证:

(3)若


正确答案
见解析。
解析
(1)




又

∴
(2)


则
∴



∴
又
∴
(3)在直角梯形



则四边形
在

故
∵

∴



∴
知识点
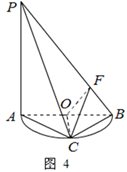
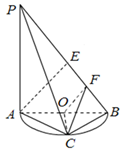
图4,PA垂直于⊙O所在平面ABC,AB为⊙O的直径,PA=AB=2,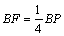
(1)证明:BC平面PAC;
(2)证明:CFBP;
(3)求四棱锥C—AOFP的体积.
正确答案
见解析。
解析
(1)
证明:∵PA⊥平面ABC,BC⊥平面ABC,
∴BC⊥PA.
∵△ACB是直径所对的圆周角,
∴
又∵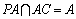
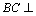
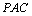
(2)证明:∵PA⊥平面ABC,OC⊥平面ABC,
∴OC⊥PA.
∵C是弧AB的中点,
∴△ABC是等腰三角形,AC=BC,
又O是AB的中点,∴OC⊥AB.
又∵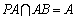
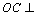
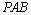
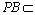
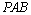
∴
设BP的中点为E,连结AE,则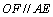
∴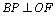
∵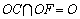
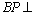
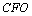
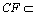
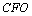
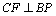
(3)解:由(2)知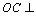
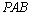
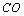

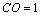
又∵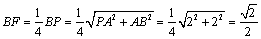
∴
又∵
∴四棱锥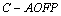
知识点
扫码查看完整答案与解析