- 解三角形
- 共459题
△ABC的内角A,B,C的对边分别为a,b,c,若

正确答案
知识点
9.在


正确答案
解析
设






考查方向
解题思路
由正弦定理,知

易错点
对正弦定理理解出现错误、计算错误
知识点
12.已知


正确答案
解析
由正弦定理得:



考查方向
本题主要考查了解三角形/本题主要考查了解三角形,在高考题中几乎每年都出现,大多考查面积计算、边和角的计算,主要考查正弦定理和余弦定理的应用,属于中档题。
解题思路
易错点
在将条件统一时,搞不清是统一成角还是统一成边运算。
知识点
14. 已知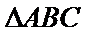
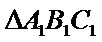
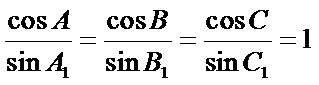
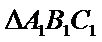
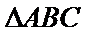
(i) 在满足下述条件的三角形中,存在“友好”三角形的是____:(请写出符合要求的条件的序号)
①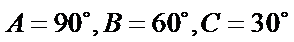
②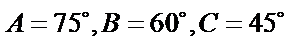
③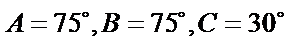
(ii) 若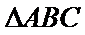
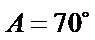
正确答案
②;
解析
(i) ①因为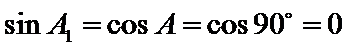
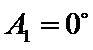
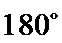
②因为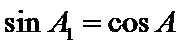
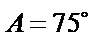
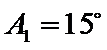
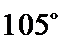
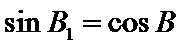
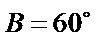
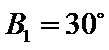
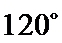
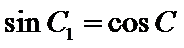
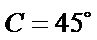
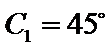
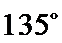

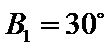
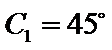
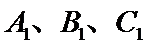
③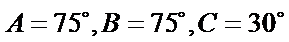
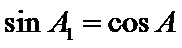
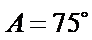
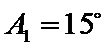
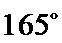
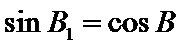
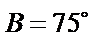
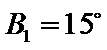
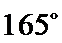
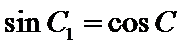
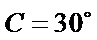
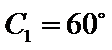
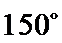
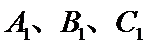
(ii)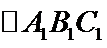
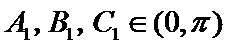
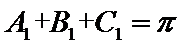
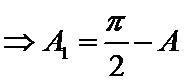
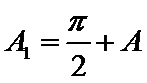
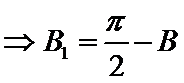
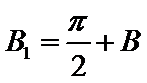

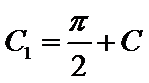
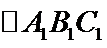
a.三个“-”;
b.三个“+”;
c.两个“-”一个“+”;
d.两个“+”一个“-”.
a.三个“-”;
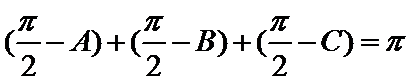
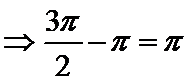
b.三个“+”;
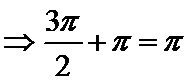
c.两个“-”一个“+”;
不妨设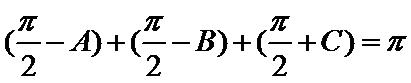
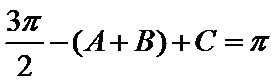
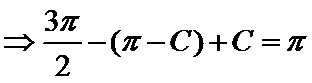
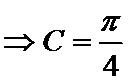
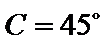
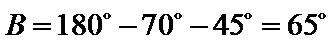
d.两个“+”一个“-”.
不妨设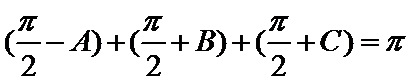

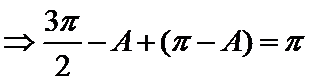
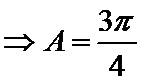
考查方向
本题考查了诱导公式,分类讨论思想,在近几年的各省高考题出现的频率较低.
解题思路
由方程、诱导公式解得
易错点
没有检查三角能不能构成三角形致误.
知识点
15. 在

(1)求
(2)若点D在


正确答案
见解析
解析
解:如图, 设




又由正弦定理得
由题设知

在

考查方向
解题思路
(1)用余弦定理求a
(2)由正弦定理求sinB
(3)在
易错点
忽略数形结合思想在本题中的作用。
知识点
16. 已知函数


(1)求
(2)3


正确答案
(1)
(2)
解析
试题分析:本题属于三角函数的图像与性质及正余弦定理的综合应用问题,属于简单题,只要掌握相关函数的知识,即可解决本题,解析如下:
(1)因为

所以

解
得:
所以函数
(2) 因为
由正弦定理,
得
因为

所以


所以

根据正弦函数的图象可以看出,


此时

所以
考查方向
本题考查了三角恒等变换、三角函数的图像及性质、利用正余弦定理判断三角函数的形状等知识点,属于简单题,只要掌握这些知识点,就可做对本题。
易错点
相关知识点不熟悉导致出错。
知识点
17.在△ABC中,角A,B


(1)求角A的值;
(2)若∠B =

正确答案
(1)
得
化简得,
(2)可知三角形ABC为等边三角形,
在三角形AMC中,
由余弦定理,
可得
解得,AC=b=2,
所以,
解析


化简得,A=30度,
可知三角形ABC是等腰三角形,
由余弦定理可得,b=2,
所以面积为
考查方向
本题主要考查正弦定理和余弦定理的性质,属于基础题
解题思路
先用正弦定理求A,然后利用余弦定理求三角形的面积
易错点
混淆两个定理的性质
知识点
19.(1)求证:sinα·sinβ=
(2)在锐角△ABC中,∠ A=60°,BC=2,求△ABC面积的取值范围.
正确答案
(1)略;(2)
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难.
(1)由

两式相减得:
(2)由正弦定理可知,
由
所以
考查方向
本题考查了三角函数的积化和差的证明及解三角形的问题.属于高考中的高频考点。
解题思路
本题考查三角函数问题,解题步骤如下:
(1)利用两角和差公式证明。
(2)利用正余弦定理求解。
易错点
注意锐角三角形的条件,忽视则容易出错。
知识点
7. 在



则角
正确答案
解析

∴A=30°
考查方向
本题主要考查了解三角形
解题思路
先角化边得到
易错点
本题易在利用正弦定理化三角函数为三角形边的关系上容易求错;
知识点
正确答案
知识点
扫码查看完整答案与解析