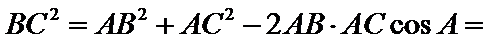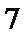- 解三角形
- 共459题
12.若锐角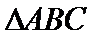
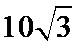
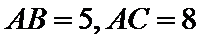
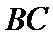
正确答案
解析
由已知得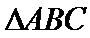
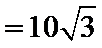
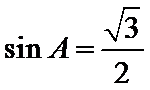
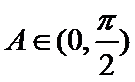

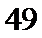
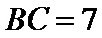
考查方向
解题思路
利用三角形的面积公式求出A,再利用余弦定理求出BC.
易错点
计算能力弱,不会用余弦定理求三角形的面积
知识点
17. 已知向量

(I)求函数
(II)在




正确答案
(1)


(2)
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求解:(I)
=
由
可得
所以函数的单调递增区间为[
(II)
由
考查方向
解题思路
本题考查三角函数与解三角形,解题步骤如下:
1、利用向量的数量积求出
2、利用余弦定理求出
易错点
第一问中的辅助角容易计算错误
知识点
9.在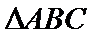
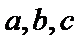
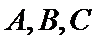
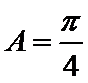
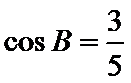
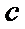
正确答案
解析
在三角形中,利用三角形的内角和A+B+C= 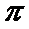
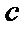
考查方向
解题思路
画出草图,标出已知信息,根据已知元素,合理准确地使用正、余弦定理求解。
易错点
根据已知额信息,不能如何准确地使用正、余弦定理求解。
知识点
16. 在△ABC中,角A,B,C的对边分别为a,b,c,向量

(Ⅰ)求角
(Ⅱ)若a=6,求△ABC面积的最大值.
正确答案
(1)

解析
试题分析:本题属于向量结合三角函数以及解三角形的知识
(1)根据向量共线的坐标表示得到一个等式,再利用正弦定理实现边角互化从而可以解出角A;
(2)先由余弦定理再结合基本不等式即可。
(Ⅰ)因为向量

所以

即
由于B是三角形的内角,


(Ⅱ)因为
所以
且仅当b=c时取得等号,所以

所以当b=c时,△ABC面积的最大值为
考查方向
解题思路
本题考查向量结合三角函数以及解三角形的知识,解题步骤如下:
(1)根据向量共线的坐标表示得到一个等式,再利用正弦定理实现边角互化从而可以解出角A;
(2)先由余弦定理再结合基本不等式即可。
易错点
不能联想到基本不等式。
知识点
如图,在四边形





16.求
17.若

正确答案
见解析
解析
(Ⅰ)
因为

所以△ACD的面积
考查方向
解题思路
利用已知条件求出∠D角的正弦函数值,然后求
易错点
主要易错于计算出错,
正确答案
见解析
解析
(Ⅱ)在△ACD中,
所以
在△ABC中,
把已知条件代入并化简得:

考查方向
解题思路
利用已知条件求出∠D角的正弦函数值,然后求
易错点
主要易错于计算出错,
16.在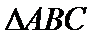
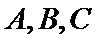
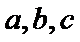
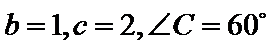
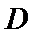
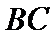
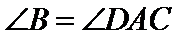
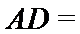
正确答案
解析
在三角形ABC中由正弦定理可以求出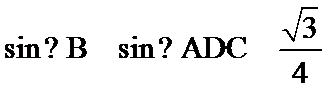
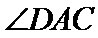
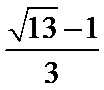
考查方向
解题思路
本题考查正余弦定理解三角形的能力,解题步骤如下:先用正弦定理求出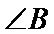
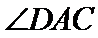
易错点
不会灵和应用定理解答。
知识点
15.在



则
正确答案
解析
因为


所以

考查方向
解题思路
先根据余弦定理表示出
易错点
利用定理进行恒等变换时错误
知识点
已知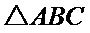
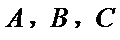
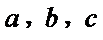
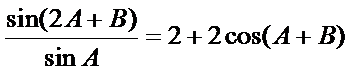
17.求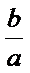
18.若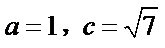
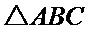
正确答案
(1)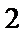
解析
(Ⅰ)∵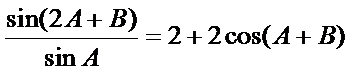
∴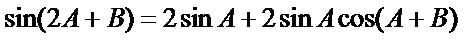
∴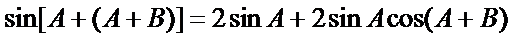
∴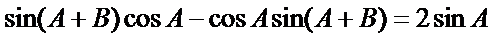
∴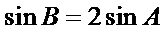
∴
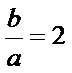
考查方向
解题思路
1)第一问中用两角和差公式和三角恒等变换化简得到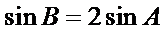
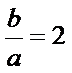
2)第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
1)第一问中想不到将角
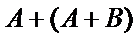
2)第二问中用余弦定理求角时容易将特殊角记错。
正确答案
(2)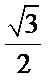
解析
(Ⅱ)∵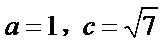
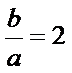
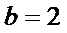
∴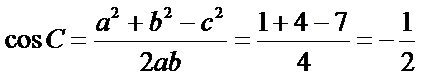
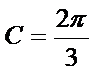
∴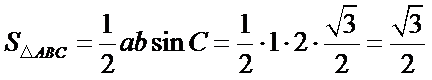
即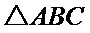
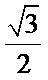
考查方向
解题思路
1)第一问中用两角和差公式和三角恒等变换化简得到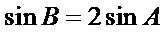
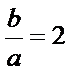
2)第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
1)第一问中想不到将角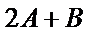
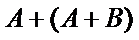
2)第二问中用余弦定理求角时容易将特殊角记错。
男性,60岁,在接受前列腺痛根治术2年后发现股骨和腰椎骨转移性痛,已接受过雌激素治疗。病人出现疲倦、乏力、恶心、呕吐、头痛、口渴、多尿等情况。病人可能发生
A.高渗性缺水
B.水过多
C.低钙血症
D.高钙血症
E.镁过多
正确答案
D
解析
暂无解析
设




正确答案
解析


因为



知识点
扫码查看完整答案与解析