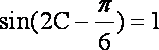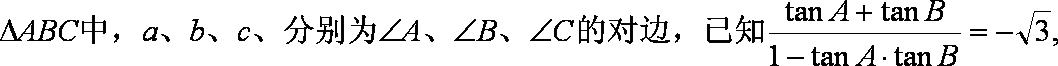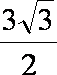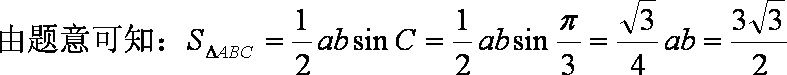- 解三角形
- 共459题
已知





(1)求:
(2)若



正确答案
(1)4(2)
解析
解析:(1)由正弦定理

又

可得
(2)若







由正弦定理


知识点
已知a,b,c分别是△ABC的三个内角A,B,C的对边,若向量



(1)求角A的大小;
(2)求函数
正确答案
见解析。
解析
(1)因为向量



所以(2b﹣c)cosA=acosC,由正弦定理得:2sinBcosA=sinCcosA+sinAcosC=sin(A+C)
即2sinBcosA=sinB,所以cosA=

(2)因为函数


而

知识点
在





正确答案
见解析。
解析
因为


又因为

由余弦定理得:

即
解得

知识点
在


(1)求
(2)若
正确答案
见解析。
解析
(1)∵
由余弦定理得
故
(2)∵
∴
∴
∴
∴

又∵
故
知识点
已知△ABC中,角A、B、C的对边分别
(1)求
(2)求
正确答案
见解析。
解析
(1)
由余弦定理得
(2)由正弦定理知:
知识点
已知函数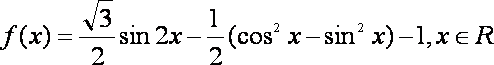
(1)求函数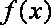
(2)设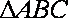
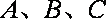
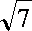
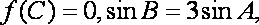

正确答案
见解析。
解析
(1)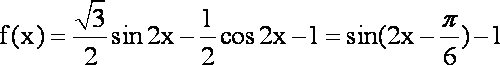

(2)由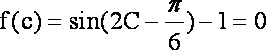
又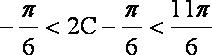
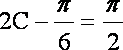
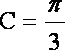
由余弦定理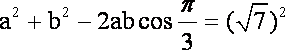
由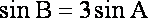
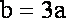
由①②得,a=1,b=3………………………………………………………………………12分
知识点




若




(1)求A,B,C;
(2)若函数



正确答案
见解析。
解析
(1)根据题意得


∴


(2)∵



又∵



由
知识点
在

(1)求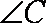
(2)求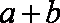
正确答案
见解析。
解析
(1)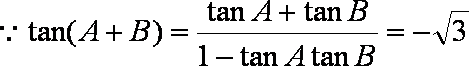
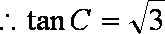

又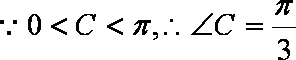
(2)
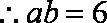
由余弦定理可得: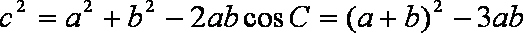
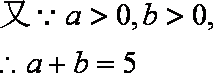
知识点
在


(1)求角C
(2)求
正确答案
见解析
解析
解析:
(1)

所以


(2)
因为





故

知识点
甲地与乙地相距250公里,某天小袁从上午7∶50由甲地出发开车前往乙地办事,在上午9∶00,10∶00,11∶00三个时刻,车上的导航仪都提示“如果按出发到现在的平均速度继续行驶,那么还有1小时到达乙地”,假设导航仪提示语都是正确的,那么在上午11∶00时,小袁距乙地还有 ▲ 公里。
正确答案
60
解析
设从出发到上午11时行了


知识点
扫码查看完整答案与解析