- 三角函数的最值
- 共80题
14.在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是
正确答案
8
知识点
15.函数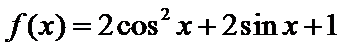
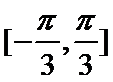
正确答案
解析
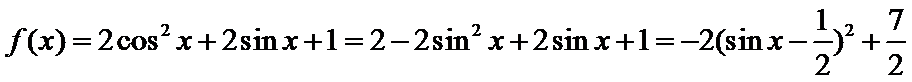
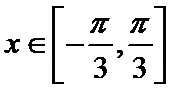
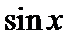
考查方向
解题思路
本题属于简单题,
(1)利用同角三角函数的关系化成同一三角函数并配方
(2)利用二次函数的图像求最值
易错点
利用二次函数的图像求最值
知识点
(14分)(2015•上海)如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
(1)求t1与f(t1)的值;
(2)已知警员的对讲机的有效通话距离是3千米.当t1≤t≤1时,求f(t)的表达式,并判断f(t)在[t1,1]上的最大值是否超过3?说明理由.
正确答案
解:(1)由题意可得t1=

设此时甲运动到点P,则AP=v甲t1=5×

∴f(t1)=PC=
=

(2)当t1≤t≤
∴QB=AC+CB﹣8t=7﹣8t,PB=AB﹣AP=5﹣5t,
∴f(t1)=PC=
=

(2)当t1≤t≤
∴QB=AC+CB﹣8t=7﹣8t,PB=AB﹣AP=5﹣5t,
∴f(t)=PQ=
=
=
当
∴f(t)=PB=AB﹣AP=5﹣5t
∴f(t)=
∴当

故f(t)的最大值超过了3千米.
知识点
15.已知函数
(Ⅰ)求函数
(Ⅱ)求函数

正确答案
(Ⅰ)
(Ⅱ)0
解析
(Ⅰ)因为



(Ⅱ)因为


当


当


因为
所以函数

考查方向
本题主要考察了三角函数的图象与性质,属于中档题,是高考的热点,解决此类题的关键:一是会化简,熟悉三角恒等变形公式;二是会用性质,熟悉单调性、周期性、对称性、和最值问题。
易错点
1、本题易在化简的过程汇总发生错误,导致最小正周期算错 。
2、单调性分析不全面,导致题目无法进行。
知识点
17.设函数
(1)求函数
(2)若





正确答案
(1)


(2)

解析
试题分析:本题属于三角函数的图像与性质及正余弦定理的综合应用问题,属于简单题,只要掌握相关三角函数的知识,即可解决本题,解析如下:
试题解析:(1)
∴函数f(x)的最小正周期
当

当

(2)因为

∴


∵
由余弦定理得:
∴
考查方向
解题思路
(1)先用两角和与差的正弦化简
(2)先根据解析式求得角


易错点
相关知识点不熟容易证错。
知识点
扫码查看完整答案与解析