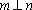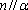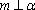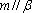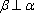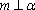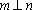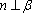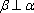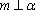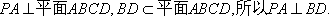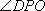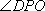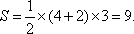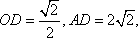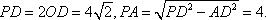空间中直线与平面之间的位置关系
共25题

· 空间中直线与平面之间的位置关系

空间中直线与平面之间的位置关系
共25题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设是两条不同的直线，是两个不同的平面（）

A若，，则

B若，则

C若则

D若，，，则

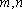
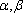
正确答案

解析

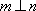
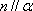
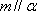
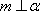
对A，若，，则或或，错误；

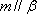
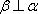
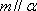
对B，若，，则或或，错误；

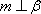
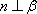
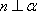
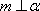
对C，若，，，则，正确；

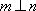
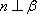
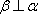
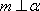
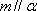
对D，若，，，则或或，错误.

故选C. 点评：本题考查空间中的线线、线面、面面的闻之关系，容易题

知识点

空间中直线与平面之间的位置关系直线与平面平行的判定与性质直线与直线垂直的判定与性质

题型：简答题

简答题 · 12 分

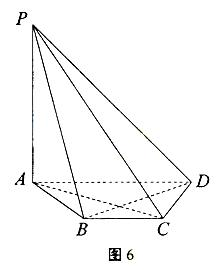
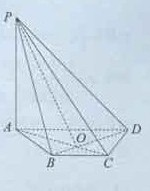
如图6，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是等腰梯形，AD∥BC，AC⊥BD.

（1）证明：BD⊥PC；

（2）若AD=4，BC=2，直线PD与平面PAC所成的角为30°，求四棱锥P-ABCD的体积.

正确答案

见解析

解析

（1）因为

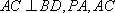
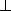
又是平面PAC内的两条相较直线，所以BD平面PAC，

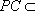
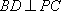
而平面PAC，所以.

（2）

设AC和BD相交于点O，连接PO，由（1）知，BD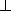平面PAC，

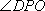
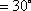
所以是直线PD和平面PAC所成的角，从而.

由BD平面PAC，平面PAC，知.

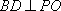
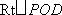
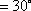
在中，由，得PD=2OD.

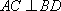
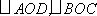
因为四边形ABCD为等腰梯形，，所以均为等腰直角三角形，

从而梯形ABCD的高为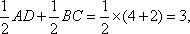于是梯形ABCD面积

在等腰三角形ＡＯＤ中，

所以

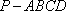
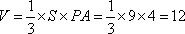
故四棱锥的体积为.

知识点

空间中直线与平面之间的位置关系

题型：简答题

简答题 · 14 分

如图，在三棱锥中，，，°，平面平面，，分别为，中点。

（1）求证：∥平面；

（2）求证：；

（3）求三棱锥的体积。

正确答案

见解析

解析

（1）因为，分别为，中点，

所以∥，

又平面，平面，

所以∥平面. …………………4分

（2）连结，

因为∥，又°，

所以.

又，为中点，所以.

所以平面，所以. …………………9分

（3）因为平面平面，有，

所以平面，

所以. …………14分

知识点

空间中直线与平面之间的位置关系

题型：单选题

单选题 · 5 分

已知正四棱柱中，，，为的中点，则直线与平面的距离为

正确答案

解析

因为底面的边长为2，高为，且连接，得到交点为，连接，，则点到平面的距离等于到平面的距离，过点作，则即为所求，在三角形中，利用等面积法，可得，故选答案D。

知识点

空间中直线与平面之间的位置关系

题型：简答题

简答题 · 12 分

如图在直菱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=，AA1=3，D是BC的中点，点E在菱BB1上运动。

（1）证明：AD⊥C1E；

（2）当异面直线AC，C1E 所成的角为60°时，求三菱子C1-A2B1E的体积

正确答案

见解析

解析

（1）.

(证毕)

（2）.

知识点

空间中直线与平面之间的位置关系

题型：简答题

简答题 · 14 分

如图，在三棱柱中，底面，，E、F分别是棱的中点。

（1）求证：AB⊥平面AA1 C1C；

（2）若线段上的点满足平面//平面，试确定点的位置，并说明理由；

（3）证明：⊥A1C.

正确答案

见解析

解析

（1）底面，

， ---------------------2分

，，

面. -------------------4分

（2）面//面，面面，面面，

//， ---------------7分

在中是棱的中点，

是线段的中点. ------------8分

（3）三棱柱中

侧面是菱形，， -------------------------9分

由（1）可得，

，面， ------------------11分

. ----------------12分

又分别为棱的中点，

//， -----------------13分

. ----------------14分

知识点

空间中直线与平面之间的位置关系

题型：简答题

简答题 · 12 分

如图，、为圆柱的母线，是底面圆的直径，、分别是、的中点，。

（1）证明：；

（2）证明：；

（3）求四棱锥与圆柱的体积比。

正确答案

见解析。

解析

（1）证明：连结，.分别为的中点，∴. 又，且.∴四边形是平行四边形，即. ∴.

（2）证明：、为圆柱的母线，所以且，即，

又是底面圆的直径，所以，，所以

由，所以，，

所以……9分

（3）解：由题，且由（1）知.∴，∴ ，∴.

因是底面圆的直径，得，且，

∴，即为四棱锥的高，设圆柱高为，底半径为，

则，∴：.

知识点

空间中直线与平面之间的位置关系

题型：单选题

单选题 · 5 分

已知是两条直线，是两个平面，给出下列命题：①若，则；②若平面上有不共线的三点到平面的距离相等，则；③若为异面直线，则，其中正确命题的个数

A个

B个

C个

D个

正确答案

解析

略

知识点

空间中直线与直线之间的位置关系空间中直线与平面之间的位置关系平面与平面之间的位置关系

题型：填空题

填空题 · 5 分

下列命题：

①如果一个平面内有一条直线与另一个平面内的一条直线平行，那么这两个平面平行；

②如果一个平面内的两条直线分别平行于另一个平面，那么这两个平面平行；

③平行于同一平面的两个不同平面相互平行；

④垂直于同一直线的两个不同平面相互平行。

其中真命题的是。（把正确的命题序号全部填在横线上）

正确答案

解析

略

知识点

空间中直线与平面之间的位置关系

题型：简答题

简答题 · 14 分

如图,在四棱锥E-ABCD中,底面ABCD为正方形, AE⊥平面CDE,已知AE=3,DE=4。

（1）若F为DE的中点,求证:BE//平面ACF；

（2）求直线BE与平面ABCD所成角的正弦值。

正确答案

见解析。

解析

（1）设AC与BD相交于G,连结GF。

正方形ABCD,,又,

,2分

平面ACF,平面ACF,

平面ACF 3分

（2）解法一:过E点作EH⊥AD,垂足为H,连结BH1分

平面CDE,,又,,

平面ADE,,,平面ABCD,

所以是直线BE与平面ABCD所成的角，4分

Rt中,AE=3,DE=4,。,

所以直线BE与平面ABCD所成角的正弦值为， 4分

解法二:平面CDE,,又,,

平面ADE, ,, Rt中,AE=3,DE=4,,即,

设直线BE与平面ABCD所成角为,

所以直线BE与平面ABCD所成角的正弦值为，4分

知识点

空间中直线与平面之间的位置关系直线与平面平行的判定与性质

继续学习学习下一知识点

下一知识点 : 平面与平面之间的位置关系

百度题库 > 高考 > 文科数学 > 空间中直线与平面之间的位置关系

扫码查看完整答案与解析