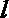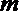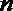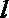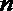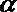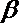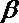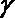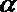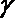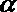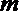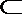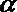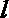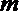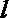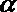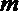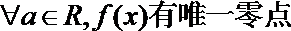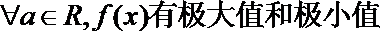- 命题的真假判断与应用
- 共152题
5．已知命题
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15． 已知
①
② 
③ 
④
⑤ 点
则正确的命题是 _____________．（写出所有正确命题的编号）。
正确答案
①③⑤
解析
解析已在路上飞奔，马上就到！
知识点
9． 有下列四个命题：
①对于
②所有指数函数的图象都经过点
③若实数
④已知两个非零向量
其中真命题的个数（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．设函数
①
②
③
④当
其中所有正确命题的序号是__________．
正确答案
①④
解析
解析已在路上飞奔，马上就到！
知识点
15．给出下列几个命题：
①若函数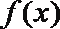
②若函数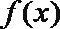
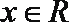
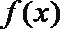
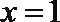
③已知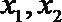
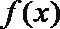
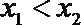
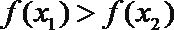
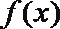
④设函数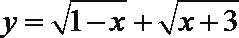
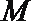
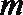
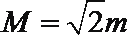
⑤若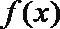
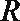
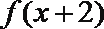
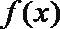
其中正确的命题序号是___________．（写出所有正确命题的序号）
正确答案
①④⑤
解析
解析已在路上飞奔，马上就到！
知识点
15．已知函数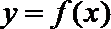
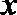
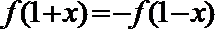
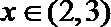
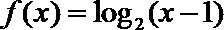
① 函数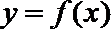
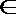
② 函数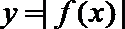
③ 当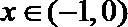
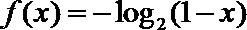
④ 函数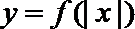
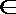
其中所有正确结论的序号为
正确答案
①②③
解析
解析已在路上飞奔，马上就到！
知识点
6．设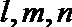
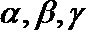
A若
B若
C若
D若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．给出以下结论：
①甲从四面体中任意选择一条棱，乙也从该四面体中任意选择一条棱，则所得的两条棱所在的直线是异面直线的概率是
②关于x的不等式
③若关于x的方程
④函数
其中正确的结论是___________（填上所有正确结论的序号）
正确答案
①④
解析
解析已在路上飞奔，马上就到！
知识点
9．已知函数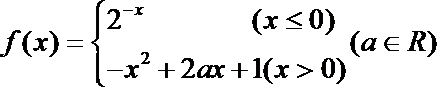
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15.现有下列命题：
①命题“
②若
③函数
④若非零向量
其中正确命题的序号有__________。
正确答案
②③
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析