- 命题的真假判断与应用
- 共152题
在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为P(

①若点A的“伴随点”是点A′,则点A′的“伴随点”是点A.
②单位圆上的点的“伴随点”仍在单位圆上;
③若两点关于x轴对称,则它们的“伴随点”关于y轴对称;
④若三点在同一条直线上,则它们的“伴随点”一定共线.
其中的真命题是 (写出所有真命题的序号).
正确答案
②③
知识点
6.下列说法错误的是( )
正确答案
解析
A.若










即

∴所以选项C为正确选项
考查方向
解题思路
逐个选项验证,分别判断它们的正误,其中ABD均正确,选项C的a值不能使两者同时成立,故可得答案.
易错点
本题易在充分必要条件的判定混淆使用
知识点
4.下列结论正确的是( )
正确答案
解析
根据否命题是条件结论全否,所以A错。
特例




特称命题的否定是全称命题,且否定结论,所以C错
命题“


考查方向
解题思路
1)否命题是条件结论全否,命题的否定是只否定结论,对A C D进行选择
2)使用充分,必要条件的判定对BC进行排除
易错点
本题易错于否命题和命题的否定的区别,导致无法排除
知识点
8.已知命题




正确答案
解析
因为P是真命题,所以非P为假命题,所以,
即


考查方向
命题的真假的判断
解题思路
根据题意依次判断命题真假
易错点
逻辑关系混乱
知识点
12.德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数



命题:①

理数


三个点

正确答案
解析
由于f(x)的值域是{0,1},故



考查方向
新定义函数的性质 函数的奇偶性
解三角形的性质
解题思路
根据所给的条件,然后结合选项依次判断
易错点
对新定义函数理解错误,计算能力弱
知识点
13.给出下列命题:
①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②由变量x和y的数据得到其回归直线方程L:y =bx + a,则L一定经过点P(x,y)
③从匀速传递的产品生产流水线上


④在回归分析模型中,残差平方和越小,说明模型的拟合效果越好;
⑤在回归直线方程y = 0.lx + 10中,当解释变量x每增加一个单位时,预报变量y增加0.1 个单位,
其中真命题的序号是 .
正确答案
②④⑤
解析
①线性相关系数|r|越大,两个变量的线性相关性越强,故①不正确;
②由变量x和y的数据得到其回归直线方程l:y=bx+a,则l一定经过点P故②正确;
③从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样不是分层抽样,故③不正确;
④可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,故④正确;
⑤在回归直线方程y=0.1x+10中,当解释变量x每增加一个单位时,预报变量平均增加0.1个单位,故⑤正确.
故答案为:②④⑤
考查方向
本题线性相关、回归直线方程和拟合等相关概念。
易错点
对上述概念理解的不透彻
知识点
15.设函数f (x)的定义域为I,若对
若对

①f (x) =ln(l+x)(x≠0)为
②f (x) =sinx (0<x<

③f (x)为

④


其中真命题有 .(把你认为真命题的序号都填上)
正确答案
①②④
解析
试题分析:本题属于函数图像的问题,题目的难度较大。注意严格按照题目的定义求解。
考查方向
本题主要考查了函数图像的问题。
解题思路
本题考查函数图像,解题步骤如下:依次画出①②③④中的函数图像,若满足f(x)<x,则称f(x)为T-函数;若有f[f(x)]<x,则称f(x)为
易错点
本题必须注意严格按照题目的定义求解,忽视则会出现错误。
知识点
12.已知函数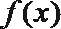
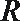
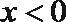
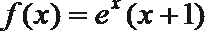
①当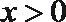
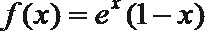
②函数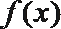
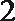
③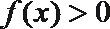
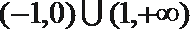
④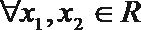
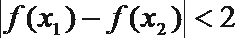
其中正确的命题是( )
正确答案
解析
当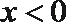
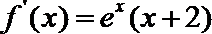
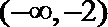
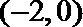
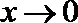
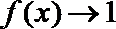
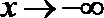
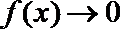
考查方向
本题主要考查函数的综合应用
解题思路
正确画出函数的图象。
易错点
1、函数性质理解不透;
2、不能正确的分析出函数的基本形式。
知识点
5.设l是直线,α和β是平面,则下列说法正确的是( )
正确答案
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是简单。
考查方向
本题主要考查了线面位置关系,在近几年的各省高考题出现的频率较高。
解题思路
本题考查线面位置关系,解题步骤如下:
由题可知,A中可能l∥β;B中可能l在β内;C中可能α⊥β。
易错点
本题易在判断线是否在面上发生错误。
知识点
5.已知三条不重合的直线

正确答案
解析
若m∥n,n⊂α,则m∥α,或m⊂α,或A不正确;
若α⊥β,α∩β=m,n⊥m,则n与α相交或n∥α或n⊂α,故B不正确;
若l⊥n,m⊥n,则l与m相交、平行或异面,故C不正确;
若l⊥α,m⊥β,且l⊥m,则由直线垂直于平面的性质定理和平面与平面垂直的判定定理知α⊥β,故D正确.
考查方向
本题主要考查了空间中直线与平面之间的位置关系.
解题思路
直接按照对直线与直线、直线与平面、平面与平面的位置关系直接判断的概念逐条判断
易错点
本题易在对直线与直线、直线与平面、平面与平面的位置关系直接判断的概念上理解不透;
知识点
扫码查看完整答案与解析














































