命题的真假判断与应用
共152题

· 命题的真假判断与应用

命题的真假判断与应用
共152题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

18．下列四个命题：

①函数的值域是(-∞，-2]∪[2，+∞)；

②命题与命题，若是的充分不必要条件，则是的充分不必要条件；

③函数的图象经过第一象限；

④函数的反函数是；

其中正确命题的序号是____________。（把你认为正确的序号都填上）。

正确答案

①④

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用

题型：单选题

单选题 · 5 分

6．已知函数，下面结论错误的是（）

A函数的最小正周期为

B函数是偶函数

C函数的图象关于直线对称

D函数在区间上是增函数

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用三角函数的周期性及其求法余弦函数的奇偶性余弦函数的单调性诱导公式的作用

题型：填空题

填空题 · 5 分

16．给出下列三个命题：

①函数与是同一函数；

②若函数与的图像关于直线对称，则函数与的图像也关于直线对称；

③若奇函数对定义域内任意都有，则为周期函数；其中真命题是（）.

正确答案

②③

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用判断两个函数是否为同一函数函数奇偶性的性质函数的周期性反函数

题型：单选题

单选题 · 5 分

2. 以下判断正确的是（）

A命题“负数的平方是正数”不是全称命题

B命题“”的否定是“”

C“”是“函数的最小正周期是”的必要不充分条件

D“”是“函数是偶函数”的充要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定命题的否定命题的真假判断与应用全（特）称命题的否定

题型：单选题

单选题 · 4 分

18．若是定义在上的奇函数，且时，有如下命题：

①时，；

②在上递增；

③的反函数的定义域是；

④函数的图像与函数的图像关于点对称，

则以上各命题中正确的个数是（）

A4个

B3个

C2个

D1个

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用函数性质的综合应用

题型：填空题

填空题 · 5 分

15.设和为不重合的两个平面，给出下列命题：

①若内的两条相交直线分别平行于内的两条直线，则∥；

②若外的一条直线与内的一条直线平行，则∥；

③设，若内有一条直线垂直于，则；

④直线的充要条件是与内的两条直线垂直.

其中所有的真命题的序号是__________ .

正确答案

①②

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用直线与平面平行的判定与性质平面与平面平行的判定与性质直线与平面垂直的判定与性质平面与平面垂直的判定与性质

题型：单选题

单选题 · 5 分

5．给出如下四个命题：

①若“”为真命题，则均为真命题；

②“若”的否命题为“若，则”；

③“”的否定是“”；

④“”是 “”的充要条件．

其中不正确的命题是（）

A①②

B②③

C①③

D③④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断充要条件的判定命题的否定命题的真假判断与应用

题型：单选题

单选题 · 5 分

4．给出如下四个命题：

①若“”为假命题，则均为假命题;

②命题“若a>b，则”的否命题为“若a≤b，则”；

③命题“任意”的否定是“存在”；

④在△ABC中，“A>B“是“sin A>sin B”的充要条件．

其中不正确命题的个数是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定命题的否定命题的真假判断与应用

题型：单选题

单选题 · 5 分

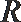
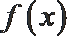
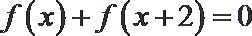
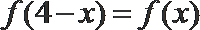
11．定义在实数集上的函数满足，且.

现有以下三种叙述：

①是函数的一个周期；

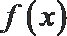
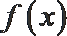
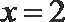
②的图象关于直线对称；

③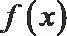是偶函数.

其中正确的是（）

A②③

B①②

C①③

D①②③

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用函数奇偶性的判断奇偶函数图象的对称性函数的周期性

题型：填空题

填空题 · 5 分

16．给出下列四个命题：

①

②，使得成立；

③为长方形，，，为的中点，在长方形内随机取一点，取得的点到距离大小1的概率为；

④在中，若，则是锐角三角形，

其中正确命题的序号是（）

正确答案

①②④

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用含有逻辑联结词命题的真假判断两角和与差的正切函数与面积、体积有关的几何概型

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 文科数学 > 命题的真假判断与应用

扫码查看完整答案与解析