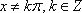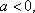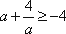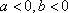- 命题的真假判断与应用
- 共152题
已知f(x)＝m(x－2m)(x＋m＋3)，g(x)＝2x－2，若同时满足条件：
①
②
则m的取值范围是________。
正确答案
(－4，－2)
解析
(一)由题意可知，m≥0时不能保证对
(1)当m＝－1时，f(x)＝－(x＋2)2，g(x)＝2x－2，此时显然满足条件①；
(2)当－1＜m＜0时，2m＞－(m＋3)，要使其满足条件①，
则需
(3)当m＜－1时，－(m＋3)＞2m，要使其满足条件①，
则需
因此满足条件①的m的取值范围为(－4,0)。
(二)在满足条件①的前提下，再探讨满足条件②的m的取值范围。
(1)当m＝－1时，在(－∞，－4)上，f(x)与g(x)均小于0，不合题意；
(2)当m＜－1时，则需2m＜－4，即m＜－2，所以－4＜m＜－2；
(3)当－1＜m＜0时，则需－(m＋3)＜－4，即m＞1，此时无解。
综上所述满足①②两个条件的m的取值范围为(－4，－2)。
知识点
)已知命题p：∀x∈R,2x＜3x；命题q：∃x∈R，x3＝1－x2，则下列命题中为真命题的是( )。
Ap∧q
B
Cp∧
D
正确答案
解析
由20＝30知，p为假命题，令h(x)＝x3－1＋x2，
∵h(0)＝－1＜0，h(1)＝1＞0，
∴x3－1＋x2＝0在(0,1)内有解。
∴∃x∈R，x3＝1－x2，即命题q为真命题，由此可知只有
知识点
对于任意实数x,符号[x]表示不超过x的最大整数,例如[-1.5]=-2,[2.5]=2,定义函数
正确答案
解析
作出函数
知识点
下列命题正确的是( )
A若
B若
C若
D若
正确答案
解析
略
知识点
命题
A“
B“
C
D
正确答案
解析
命题
知识点
扫码查看完整答案与解析