简单的线性规划
共504题

简单的线性规划
共504题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知函数在区间(0,1)内任取两个实数p,q，且p≠q，不等式恒成立，则实数的取值范围为

A[15,+∞)

B(-∞,15]

C(12,30]

D(-12,15]

正确答案

解析

由已知得，，且，等价于函数在区间上任意两点连线的割线斜率大于1，等价于函数在区间的切线斜率大于1恒成立。

，即恒成立，变形为，因为，故。

知识点

不等式恒成立问题

题型：简答题

简答题 · 14 分

20．已知函数

（1）若，求的值；

（2）若对于恒成立，求实数的取值范围

正确答案

（1）当时，；

当时，

由条件可知，

即

解得

，

（2）当时，

即

，

故的取值范围是

解析

解析已在路上飞奔，马上就到！

知识点

不等式恒成立问题其它不等式的解法

题型：简答题

简答题 · 14 分

17.已知定义域为R的函数是奇函数,其中是常数,且

（1）求的值；

（2）对任意的,不等式恒成立,求的取值范围.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的性质不等式恒成立问题

题型：填空题

填空题 · 4 分

12．在上定义运算△：，若不等式，对任意实数恒成立，则实数的取值范围是（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式恒成立问题

题型：简答题

简答题 · 14 分

21．已知定义域为的函数是奇函数

（1）求实数的值；

（2）若对于任意的，不等式恒成立，求的取值范围

正确答案

（1）是上的奇函数，

，

又，

（2）上的奇函数，

不等式等价于，

即

由（1）知，

是上为减函数

所以

即对一切有：，

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的性质不等式恒成立问题

题型：单选题

单选题 · 5 分

6. 已知函数＝－2＋3m，x∈R，若＋9≥0恒成立，则实数m的取值范围是（）

Am≥

Bm>

Cm≤

Dm<

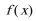
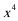
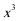
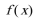
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式恒成立问题

题型：简答题

简答题 · 13 分

18.已知定义域为的函数是奇函数。

（I）求的值；

（Ⅱ）判断f(x)的单调性并说明理由；

（III）若对任意的，不等式恒成立，求的取值范围；

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明函数奇偶性的性质不等式恒成立问题

题型：单选题

单选题 · 5 分

10.函数，当时，有恒成立，则实数m的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式恒成立问题

题型：填空题

填空题 · 5 分

14．已知函数，对于上的任意，有如下条件：

①； ②； ③．

其中能使恒成立的条件序号是__________．

正确答案

②

解析

解析已在路上飞奔，马上就到！

知识点

不等式恒成立问题

题型：简答题

简答题 · 18 分

23．已知函数（常数）的图像过点．两点。

（1）求的解析式；

（2）若函数的图像与函数的图像关于直线对称，若不等式恒成立，求实数的取值范围；

（3）若是函数图像上的点列，是正半轴上的点列，为坐标原点，是一系列正三角形，记它们的边长是，探求数列的通项公式，并说明理由。

正确答案

（1）把和

分别代入

可得：

化简此方程组

可得：

即

可得，

，

代入原方程组可得：

（2）由题意知：为的反函数，

（）

即当恒成立

即当恒成立，

只需求函数在上的最小值即可，

又在单调递增，

，

（3）由联立可解得：，

即，

----12’

的边长为，

此三角形的高即点的纵坐标为

，

，两式相减可得：

即数列为公差为的等差数列

又，

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法数列与函数的综合不等式恒成立问题

继续学习学习下一知识点

下一知识点 : 基本不等式及不等式的应用

百度题库 > 高考 > 理科数学 > 简单的线性规划

扫码查看完整答案与解析