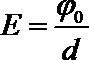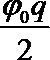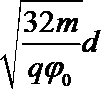- 匀变速直线运动规律的综合运用
- 共190题
4.一辆汽车以10m/s的速度沿平直公路匀速运动,司机发现前方有障碍物立即减速,以0.2m/s2的加速度做匀减速运动,减速后一分钟内汽车的位移是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图所示,物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=2m,BC=3m,且物体通过AB、BC、CD所用的时间相等,则下列说法正确的是( )
正确答案
解析
多选题
知识点
11.某航母舰载机降落在航母甲板上时着舰初速度为30m/s,此时若飞机尾部挂钩能够顺利钩住舰面上的拦阻索,飞机就能在3s内停下来。若飞机着舰时没有钩住拦阻索,飞机必须在甲板有限的200m 距离内加速到50m/s离舰复飞升空,然后准备第二次着舰降落。求:
(1)飞机钩住舰面上的拦阻索后减速过程中的加速度大小和位移大小。
(2)若飞机着舰时没有钩住拦阻索,在甲板上加速的加速度至少是多少?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24. 如图所示,公路上有一辆公共汽车以10m/s的速度匀速行驶,为了平稳停靠在站台,在距离站台P左侧位置50m处开始刹车做匀减速直线运动。同时一个人为了搭车,从距站台P右侧位置30m处从静止正对着站台跑去,假设人先做匀加速直线运动,速度达到4m/s后匀速运动一段时间,接着做匀减速直线运动,最终人和车到达P位置同时停下,人加速和减速时的加速度大小相等。求:
(1)汽车刹车的时间;
(2)人的加速度的大小。
正确答案
答案已在路上飞奔,马上就到!
解析
(1)对汽车,在匀减速的过程中,有 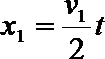
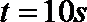
(2)设人加速运动的时间为t1,由匀变速运动规律可知:
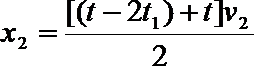
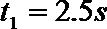
所以人的加速度大小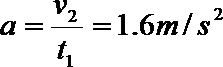
知识点
30.如图所示,质量m=0.1Kg的小球穿在长L=1.6m的斜杆上,斜杆与水平方向成α=37°角,斜杆固定不动,小球与斜杆间的动摩擦因数μ=0.75。小球受水平向左的拉力F=2N,从斜杆的顶端由静止开始下滑,求(sin370=0.6,cos370=0.8 ,g=10m/s2)
(1)小球运动的加速度大小;
(2)小球运动到斜杆底端时的速度大小。
正确答案
(1)9m/s
(2)7.8m/s
解析
解析已在路上飞奔,马上就到!
知识点
3.在地质、地震、勘探、气象和地球物理等领域的研究中,需要精确的重力加速度g值,g值可由实验精确测得,近年来测g值的一种方法叫“对称自由下落法”,它是将测g转变为测长度和时间,具体做法是:将真空长直管沿竖直方向放置,自其中O点上抛小球又落到O点的时间为T2,小球与管无碰撞。在小球运动过程中经过比O点高H的P点,小球离开P点到又回到P点所用的时间为T1,测得T1、T2和H,可求得g等于
正确答案
解析
根据竖直上抛运动的对称性可知,物体从O点竖直上抛到最高点的时间为T1,同理从P点到最高点的时间为T2,根据位置关系g(T1)2=g(T2)2+H,得g=,故选C。
考查方向
1、考查匀加速直线运动的基本公式x=v0t+at2。2、考查竖直上抛运动中对的对称性,两次经过同一点的上抛过程与下落过程的时间相等。
解题思路
1、清楚匀加速直线运动的基本公式,根据条件选择合适的公式。2、找准竖直上抛运动中的时间对称性及位置关系,根据位置关系g(T1)2=g(T2)2+H求解。
易错点
1、对计算公式的选择容易模糊不清,浪费时间。2、不清楚竖直上抛运动的对称性。
知识点
22.民用航空客机的机舱,除了有正常的舱门和舷梯连接,供旅客上下飞机外,一般还配有紧急出口.发生意外情况的飞机在着陆后,打开紧急出口的舱门,会自动生成一个气囊(由斜面部分AC和水平部分CD构成),机舱中的人可沿该气囊滑行到地面上来,如下图所示.某机舱离气囊底端的竖直高度AB=3.0 m,气囊构成的斜面长AC=5.0 m,AC与地面之间的夹角为θ. 斜面部分AC和水
正确答案
解析:人的受力如图所示,由牛顿运动定律得mgsin θ-μFN=ma
FN-mgcos θ=0
则a=gsin θ-μgcos θ=1.6 m/s2
设人在斜面部分滑下所用的时间为t1,
s=at,t1=2.5 s
设人滑到斜面底端C时的速度为vC,
vC=at1=4 m/s
由牛顿运动定律得μmg=ma′
由0-vC=(-a′)t2
解得t2=0.73 s)
故人从开始到滑到E点所用的时间t=t1+t2=3.23 s.
解析
解析已在路上飞奔,马上就到!
知识点
33.如图(a),长为L的光滑斜面AB与高台边缘光滑相接,BC为一竖直墙,将小球从斜面AB的顶端静止释放,小球到达斜面底端后恰能无能量损失地从高台边缘水平飞出.高台底部有另一足够长的斜面CD.调节斜面AB的倾角α与斜面CD的倾角β,使小球从斜面AB顶端静止释放后,恰能垂直击中斜面CD.不计空气阻力,重力加速度为g,α、β为锐角.求:
(1)小球在空中飞行时间t(用α、β和L表示)?
(2)某一研究小组取长为L=0.5m的斜面AB进行实验,实验中发现改变斜面AB的倾角α后,为了使从AB顶端静止释放的小球还能垂直击中斜面,只需对应地调整斜面CD的倾角β.多次实验并记录每次α与β的数值,由实验数据得出图(b)所示拟合直线.请问此坐标系的横轴表示什么?试求竖直墙BC的高度h(取g=10m/s2)?
(3)在第(2)问中,该研究小组发现,小球每次垂直打在CD上的落点与竖直墙BC的距离S随α和β的改变而不同.试求小球在CD上的落点离竖直墙的最大距离Sm?此时倾角α与β各为多大?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
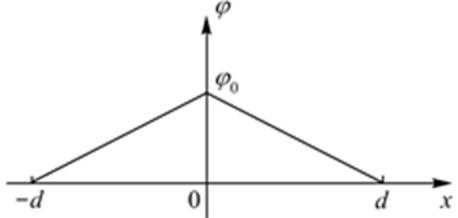
18.物理图象能简明、形象地反映某物理量随另一物理量变化的规律,故图象法在物理中有广泛的应用。如v-t图象切线的斜率反映的是物体的加速度,所围的“面积”反映的是物体运动的位移。如图所示,是一静电场中电势 随x的分布图像。已知该静电场的场强方向平行于x轴,图中φ0和d为已知量。以下判断正确的是( )
正确答案
解析
每小题给出的四个选项中,有一个或多个选项正确。全部选对的得4分,选对但不全的得2分,有选错的得0分。
知识点
26.如图所示,三个质量均为
































(1)滑块





(3)弹簧最初的弹性势能
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析