- 匀变速直线运动规律的综合运用
- 共190题
如图所示,一足够长的固定光滑斜面倾角


14.若某一时刻轻绳被拉断,求此时外力F的大小;
15.若轻绳拉断瞬间A、B的速度为3m/s,绳断后保持外力F不变,求当A运动到最高点时,A、B之间的距离。
正确答案
60N
解析
整体
A物体:
∴ 
考查方向
解题思路
对整体分析,根据牛顿第二定律求出整体的加速度,再隔离对A分析,根据牛顿第二定律求出外力F的大小.
易错点
应用牛顿定律解决两类基本问题为命题背景考查学生的推理能力和分析综合能力,关键理清物体的运动规律,结合牛顿第二定律和运动学公式进行求解.
正确答案
2.375m
解析
设沿斜面向上为正
A物体:
∵
此过程A物体的位移为
B物体:
∴两者间距为
考查方向
解题思路
根据牛顿第二定律求出绳断后A、B的加速度,结合速度时间公式求出A速度减为零的时间,从而求出这段时间内A、B的位移,根据位移关系求出A、B间的距离.
易错点
应用牛顿定律解决两类基本问题为命题背景考查学生的推理能力和分析综合能力,关键理清物体的运动规律,结合牛顿第二定律和运动学公式进行求解.
物体A的质量M=1kg,静止在光滑的水平面上的平板车B的质量为m=0.5kg、长L=1m,某时刻A以vo=4m/s向右的初速度滑上木板B的上表面,在A滑上B的同时,给B施加一个水平向右的恒定拉力F,忽略物体A的大小,已知A与B之间的动摩擦因数μ=0.2,取重力加速度g=10m/s,试求:
17.若F=5N,在施加给B的瞬间,物体A和小车B的加速度分别是多大?
18.若F=5N,物体A在小车上运动时相对小车滑行的最大距离时多大?
19.如果要使A不至于从B的右端滑落,拉力F大小应满足什么条件?
正确答案
物体A和小车B的加速度分别是2m/s2、14m/s2;
解析
F施加的瞬间,A的加速度大小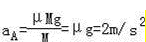
考查方向
解题思路
首先分析物体A和车的运动情况:A相对于地做匀减速运动,车相对于地做匀加速运动.开始阶段,A的速度大于车的速度,则A相对于车向右滑行,当两者速度相等后,A相对于车静止,则当两者速度相等时,物体A在小车上运动时相对小车滑行的最大距离.由牛顿第二定律和运动学公式结合,以及速度相等的条件,分别求出A与车相对于地的位移,两者之差等于A在小车上运动时相对小车滑行的最大距离.
要使A不从B上滑落,是指既不能从B的右端滑落,也不能左端滑落.物体A不从右端滑落的临界条件是A到达B的右端时,A、B具有共同的速度,根据牛顿第二定律和运动学公式结合,以及速度相等的条件,可求出此时F,为F的最小值.物体A不从左端滑落的临界条件是A到达B的左端时,A、B具有共同的速度,可求出此时F的最大值,综合得到F的范围.
易错点
牛顿定律和运动公式结合是解决力学问题的基本方法,这类问题的基础是分析物体的受力情况和运动情况,难点在于分析临界状态,挖掘隐含的临界条件
正确答案
物体A在小车上运动时相对小车滑行的最大距离为0.5m;
解析
两者速度相同时,有V0﹣aAt=aBt,得:t=0.25s
A滑行距离:SA=V0t﹣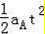
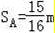
B滑行距离:SB= 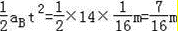
最大距离:△s=SA﹣SB=0.5m
考查方向
解题思路
首先分析物体A和车的运动情况:A相对于地做匀减速运动,车相对于地做匀加速运动.开始阶段,A的速度大于车的速度,则A相对于车向右滑行,当两者速度相等后,A相对于车静止,则当两者速度相等时,物体A在小车上运动时相对小车滑行的最大距离.由牛顿第二定律和运动学公式结合,以及速度相等的条件,分别求出A与车相对于地的位移,两者之差等于A在小车上运动时相对小车滑行的最大距离.
要使A不从B上滑落,是指既不能从B的右端滑落,也不能左端滑落.物体A不从右端滑落的临界条件是A到达B的右端时,A、B具有共同的速度,根据牛顿第二定律和运动学公式结合,以及速度相等的条件,可求出此时F,为F的最小值.物体A不从左端滑落的临界条件是A到达B的左端时,A、B具有共同的速度,可求出此时F的最大值,综合得到F的范围.
易错点
牛顿定律和运动公式结合是解决力学问题的基本方法,这类问题的基础是分析物体的受力情况和运动情况,难点在于分析临界状态,挖掘隐含的临界条件
正确答案
拉力F大小应满足1N≤F≤3N.
解析
物体A不滑落的临界条件是A到达B的右端时,A、B具有共同的速度v1,则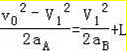
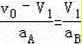
代入数据联立可得:aB=6
若F<1N,则A滑到B的右端时,速度仍大于B的速度,于是将从B上滑落,所以F必须大于等于1N.
当F较大时,在A到达B的右端之前,就与B具有相同的速度,之后,A必须相对B静止,才不会从B的左端滑落.
即有:F=(m+M)a,µMg=ma 所以:F=3N
若F大于3N,A就会相对B向左滑下.综上:力F应满足的条件是:1N≤F≤3N.
考查方向
解题思路
首先分析物体A和车的运动情况:A相对于地做匀减速运动,车相对于地做匀加速运动.开始阶段,A的速度大于车的速度,则A相对于车向右滑行,当两者速度相等后,A相对于车静止,则当两者速度相等时,物体A在小车上运动时相对小车滑行的最大距离.由牛顿第二定律和运动学公式结合,以及速度相等的条件,分别求出A与车相对于地的位移,两者之差等于A在小车上运动时相对小车滑行的最大距离.
要使A不从B上滑落,是指既不能从B的右端滑落,也不能左端滑落.物体A不从右端滑落的临界条件是A到达B的右端时,A、B具有共同的速度,根据牛顿第二定律和运动学公式结合,以及速度相等的条件,可求出此时F,为F的最小值.物体A不从左端滑落的临界条件是A到达B的左端时,A、B具有共同的速度,可求出此时F的最大值,综合得到F的范围.
易错点
牛顿定律和运动公式结合是解决力学问题的基本方法,这类问题的基础是分析物体的受力情况和运动情况,难点在于分析临界状态,挖掘隐含的临界条件
2.2015年元宵节期间人们燃放起美丽的烟火以庆祝中华民族的传统节日,按照设计,某种型号的装有烟花的礼花弹从专用炮筒中射出后,在 3s末到达离地面 90m的最高点时炸开,构成各种美丽的图案。假设礼花弹从炮筒中竖直向上射出时的初速度是v0,上升过程中所受的平均阻力大小是自身重力的k倍,那么v0和k分别等于(g取10m/s2)( )
正确答案
解析
上升过程中所受的平均阻力f=kmg,根据牛顿第二定律得:a=
根据h=
得:a=

而(k+1)g=20m/s2,所以 k=1.
所以答案为A
考查方向
解题思路
礼花弹从炮筒中竖直射出时向上做匀减速直线运动,对其进行受力分析,根据牛顿第二定律及匀减速直线运动的基本公式即可求解.
易错点
匀变速直线运动公式注意物理量的符号
知识点
14.
如图所示,倾角为α的斜面A被固定在水平面上,细线的一端固定于墙面,另一端跨过斜面顶端的小滑轮与物块B相连,B静止在斜面上.滑轮左侧的细线水平,右侧的细线与斜面平行.A、B的质量均为m.撤去固定A的装置后,A、B均做直线运动.不计一切摩擦,重力加速度为g.求:
(1)A固定不动时,A对B支持力的大小N;
(2)A滑动的位移为x时,B的位移大小s;
(3)A滑动的位移为x时的速度大小vx.
正确答案
(1)mgcos α(2)
知识点
22.(1)质量m=1.0kg的物块A(可视为质点)与轻弹簧的上端连接,弹簧下端固定在光滑斜面底端,斜面的倾斜角θ=30º。平衡时,弹簧的压缩量为x=0.20m,此时具有的弹性势能Ep=0.50J,物块A处在O时弹簧为原长,如图所示。一质量m=1.0kg物块B(可视为质点)从距离物块A为d=2.0m处从静止开始沿斜面下滑,与物体A发生碰撞后立刻一起向下运动,但不粘连,它们到达最低点后又向上运动。求物块B向上运动到达的最高点与O的距离s。g=10m/s2
(2)如图所示,弹簧的一端固定在天花板上,另一端连接一个小球,弹簧质量不计,劲度系数为k,小球(可视为质点)的质量为m,将小球竖直悬挂起来,小球平衡的位置为坐标原点O。
将小球在竖直方向拉离平衡位置后释放,小球就在竖直方向运动起来。我们知道,以小球、地球、弹簧组成的系统,动能、弹性势能和重力势能的总和保持不变。如果把弹性势能和重力势能的和称为系统的势能,并规定小球处在平衡位置时系统的势能为零,请根据“功是能量转化的量度”,求小球运动到O点下方x处时系统的势能。
正确答案
(1)解:
B物体下滑至与A碰撞前:
AB碰撞,根据动量守恒,碰后:
可得:
碰后AB和弹簧组成的系统,机械能守恒,并且AB在弹簧处分离,设AB分离瞬间速度为v’,则根据机械能守恒:
可得:
此后,B向上做匀减速运动,上升距离为:
即O与B运动的最高点之间的距离s为0.35米。
(2)解一:
小球静止时,弹簧的形变量为x0,有:
以平衡位置为零势能面,到O点下方x:
重力做功:
弹簧弹力做功
因此,在O下方x处系统势能为:
解二:当小球在竖直方向静止时,有:
当小球在竖直方向运动经过O点下方x时,所受合力大小为
此力的大小只与小球相对其平衡位置的距离x有关,这个力做功对应于系统的势能。画出合力F随x变化的图像:
图像中图线所围成的面积即为小球从x处回O点,合力F做功,
O点为系统势能零点,那么小球在x处的系统是能为:
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析


























