- 匀变速直线运动规律的综合运用
- 共190题
下列关于物体运动的描述中正确的是( )
正确答案
解析
略
知识点
水平桌面上有两个玩具车A和B,两者用一轻质细橡皮筋相连,存橡皮筋上有一红色标记R。在初始时橡皮筋处于拉直状态,A、B和R分别位于直角坐标系中的(0,2l)(0,-l,)和(0,0)点。已知A从静止开始沿y轴正向做加速度太小为a的匀加速运动:B平行于x轴朝x轴正向匀速运动。在两车此后运动的过程中,标记R在某时刻通过点(l,l)。假定橡皮筋的伸长是均匀的,求B运动速度的大小。
正确答案
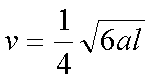
解析
设B车的速度大小为v,如图,标记R在时刻t通过点K(l,l),此时A、B的位置分别为H、G。由运动学公式,H的纵坐标yA、G的横坐标xB分别为
yA=2l+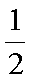
在开始运动时,R到A和B的距离之比为2:1,即OE:OF=2:1
由于橡皮筋的伸长是均匀的,在以后任一时刻R到A和B的距离之比都为2:1。
因此,在时刻t有HK:KG=2:1 ③
由于△FGH∽△IGK,有HG:KG= xB:(xB-l)④ HGKG=(yA+l):(2l) ⑤
由③④⑤式得xB=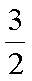
联立①②⑥⑦式得 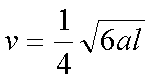
知识点
物体从A点由静止出发,做匀加速直线运动,一段时间后做匀减速直线运动,到达B点时恰好停止,则在这两个运动过程中
正确答案
解析
略
知识点
在2010年2月举行的温哥华冬奥会冰壶比赛中,我国女子冰壶队获得铜牌,显示了强大的实力。比赛场地示意如图,投掷线和营垒圆心相距s=30m,营垒半径R=1.8m,冰壶石质量均为19kg,可视为质点。某局比赛中,甲方运动员从起踏架处推着冰壶石C出发,在投掷线AB处放手让冰壶石以速度




求:
(1)若甲方运动员不刷冰,冰壶石C能滑行的最大距离是多少。
(2)为保证甲方在本局比赛中获胜,即冰壶石C不脱离营垒,冰壶石C碰撞前瞬间速度的大小;
(3)为保证甲方在本局比赛中获胜,即冰壶石C不脱离营垒,甲方运动员在投掷线AB到营垒圆心之间刷冰的最大距离是多少。
正确答案
见解析。
解析
(1)若甲方运动员不刷冰,设冰壶石滑行最大距离为s1,由动能定理得

∴ s1=29m
(2)设两冰壶石碰撞后,冰壶石C、D的速度分别是为v1、v2,考虑对方运动员刷冰,冰壶C不脱离营垒时,由动能定理得
解得:
两冰壶石相碰前,设冰壶石C的速度为
由动量守恒定律得
由能量守恒定律得
解得:
∴
(3)设甲方运动员在冰壶石碰撞前刷冰的最大距离为s2
由动能定理得
解得s2≈28.3m
知识点
下列说法正确的是
正确答案
解析
略
知识点
扫码查看完整答案与解析