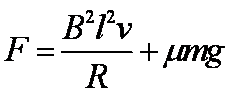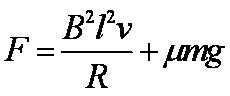- 闭合电路的欧姆定律
- 共246题
如图所示,边长为


正确答案
解析
略
知识点
如图所示的电路中,电源电动势






正确答案
0.5;
解析
略
知识点
11.如图所示,金属导轨MNC和PQD,MN与PQ平行且间距为L,所在平面与水平面夹角为α,N、Q连线与MN垂直,M、P间接有阻值为R的电阻;光滑直导轨NC和QD在同一水平面内,与NQ的夹角都为锐角θ。均匀金属棒ab和ef质量均为m,长均为L,ab棒初始位置在水平导轨上与NQ重合;ef棒垂直放在倾斜导轨上,与导轨间的动摩擦因数为μ(μ较小),由导轨上的小立柱1和2阻挡而静止。空间有方向竖直的匀强磁场(图中未画出)。两金属棒与导轨保持良好接触。不计所有导轨和ab棒的电阻,ef棒的阻值为R,最大静摩擦力与滑动摩擦力大小相等,忽略感应电流产生的磁场,重力加速度为g。
(1)若磁感应强度大小为B,给ab棒一个垂直于NQ、水平向右的速度v1,在水平导轨上沿运动方向滑行一段距离后停止,ef棒始终静止,求此过程ef棒上产生的热量;
(2)在(1)问过程中,ab棒滑行距离为d,求通过ab棒某横截面的电量;
(3)若ab棒以垂直于NQ的速度v2在水平导轨上向右匀速运动,并在NQ位置时取走小立柱1和2,且运动过程中ef棒始终静止。求此状态下最强磁场的磁感应强度及此磁场下ab棒运动的最大距离。
正确答案
(1)设ab棒的初动能为Ek, ef棒和电阻R在此过程产生的热量分别为W和W1,有
W+ W1=Ek ①
且 W=W1 ②
由题有 E1=
得 W=
说明:①②③④式各1分。
(2)设在题设工程中,ab棒滑行时间为△t,扫过的导轨间的面积为△S,通过△S的磁通量为
△φ, ab棒产生的电势能为E,ab棒中的电流为I,通过ab棒某横截面的电量为q,则
E=
且 △φ=B△S ⑥
I=
又有 I=
由图所示 △S=d(L-dcotθ) ⑨
联立⑤-⑨,解得q=
说明:⑤⑥⑦⑧⑨⑩式各1分。
(3)ab棒滑行距离为x时,ab棒在导轨间的棒长Lx为
Lx=L-2xcotθ ⑪
此时,ab棒产生的电势能Ex为 Ex =Bv2L ⑫
流过ef棒的电流Ix为 Ix= 
ef棒所受安培力Fx为 Fx=B Ix L ⑭
联立 ⑪-⑭,解得 Fx =
由⑮式可得,Fx在x=0和B为最大值Bm时有最大值F1。
由题知,ab棒所受安培力方向必水平向左,ef棒所受安培力方向必水平向右,使F1为最大值的受力分析如图所示,图中fm为最大静摩擦力,有
F1cosα=mgsinα+μ(mgcosα+ F1sinα) ⑯
联立⑮⑯,得Bm=
⑰式就是题目所求最强磁场的磁感应强度大小,该磁场方向可竖直向上,也可竖直向下。
由⑮式可知,B为Bm时,Fx随x增大而减小,x为最大xm时,Fx为最小值F2,由图可知
F2cosα+μ(mgcosα+ F2sinα)= mgsinα ⑱
联立⑮⑰⑱,得
xm=
说明:⑫⑭⑮⑯⑱⑲式各得1分,⑰2分,正确说明磁场方向得1分。
解析
解析已在路上飞奔,马上就到!
知识点
如图所示,闭合电键S,电压表的示数为U,电流表的示数为I,现向左调节滑动变阻器R的触头P,电压表V的示数改变量的大小为ΔU,电流表A的示数改变量大小为ΔI,则下列说法正确的是
正确答案
解析
略
知识点
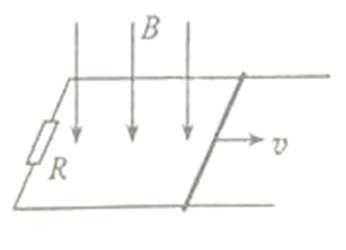
13.如图,两平行金属导轨位于同一水平面上,相距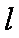
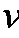
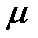
(1)电阻R消耗的功率;
(2)水平外力的大小。
正确答案
(1)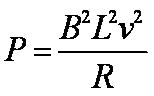
试题解析:(1)导体切割磁感线运动产生的电动势为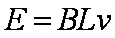
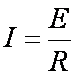
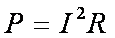
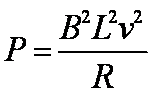
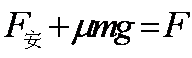
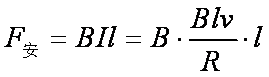
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析