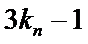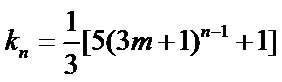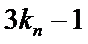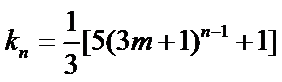- 等比数列的性质及应用
- 共180题
已知等比数列


16.求
17.若



正确答案
解析
【解析】
由题意,得



考查方向
解题思路
解题步骤如下:根据等比数列的通项公式化简等式

易错点
本题在求等比数列的公比或求数列


正确答案
解析
【解析】



考查方向
解题思路
解题步骤如下:因为





易错点
本题在求等比数列的公比或求数列


已知等差数列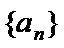
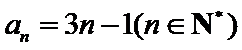
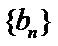
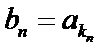
若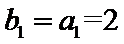
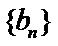
28.写出数列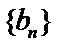
29.求数列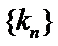
30.证明:以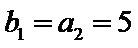
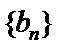
正确答案
2,8,32,128.
解析
试题分析:本题属于数列通项公式与数列求和公式的应用问题,由于问题较抽象有一定的难度。(1)求解时一定要灵活应用数学归纳法对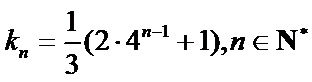
(Ⅰ)观察数列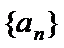
因为数列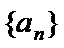
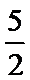
(ⅰ)以2为首项,且公比最小的等比数列的前四项是2,8,32,128.
(ⅱ)由(ⅰ)可知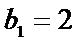
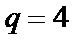
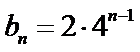
又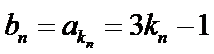
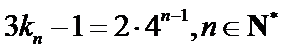
即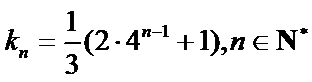
再证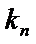
显然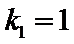
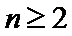
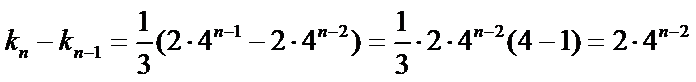
即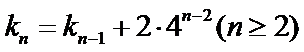
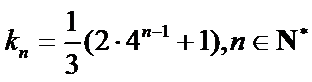
所以,所求通项公式为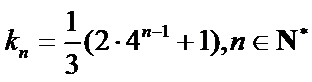
考查方向
解题思路
本题考查了等差等比数列通项公式的求解,数列求和公式的综合应用,数学归纳法和分析法的应用,解题步骤如下:
(ⅰ)根据题意写出数列的前四项是2,8,32,128.;(ⅱ)根据题意写出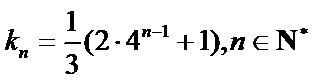
在证明“以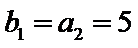
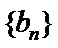
易错点
由题归纳法得数列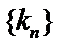
正确答案
an=22n-1;
解析
试题分析:本题属于数列通项公式与数列求和公式的应用问题,由于问题较抽象有一定的难度。(1)求解时一定要灵活应用数学归纳法对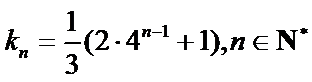
(Ⅱ)设
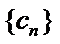
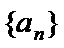
且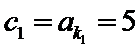
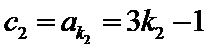
所以公比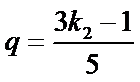
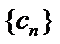
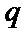
取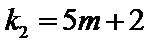
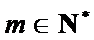
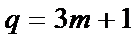
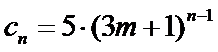
只要证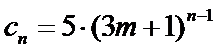
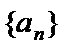
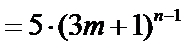
只要证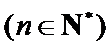
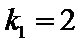
又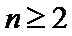
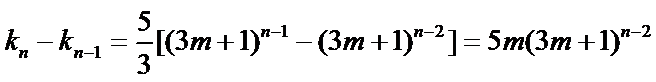
即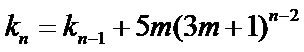
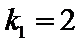
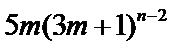

故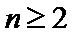
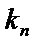
所以数列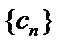
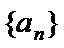
其公比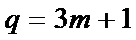
故数列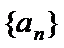
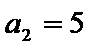
考查方向
解题思路
本题考查了等差等比数列通项公式的求解,数列求和公式的综合应用,数学归纳法和分析法的应用,解题步骤如下:
(ⅰ)根据题意写出数列的前四项是2,8,32,128.;(ⅱ)根据题意写出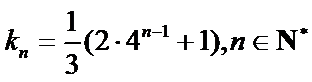
在证明“以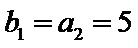
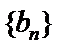
易错点
由题归纳法得数列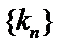
正确答案
证明略。
解析
试题分析:本题属于数列通项公式与数列求和公式的应用问题,由于问题较抽象有一定的难度。(1)求解时一定要灵活应用数学归纳法对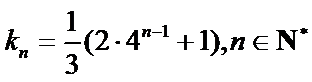
(Ⅱ)设
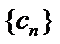
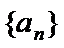
且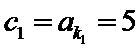
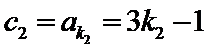
所以公比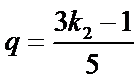
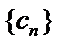
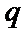
取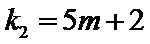
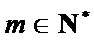
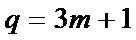
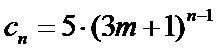
只要证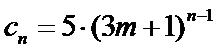
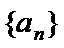
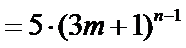
只要证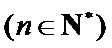
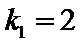
又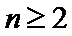
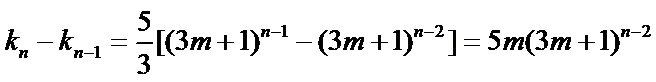
即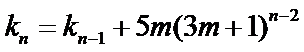
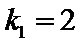
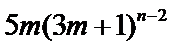

故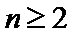
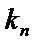
所以数列
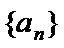
其公比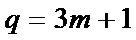
故数列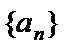
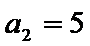
考查方向
解题思路
本题考查了等差等比数列通项公式的求解,数列求和公式的综合应用,数学归纳法和分析法的应用,解题步骤如下:
(ⅰ)根据题意写出数列的前四项是2,8,32,128.;(ⅱ)根据题意写出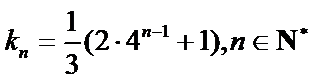
在证明“以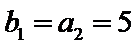
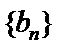
易错点
由题归纳法得数列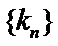
10.已知数列




正确答案
考查方向
解题思路
1. 分析


易错点
不能定量分析

知识点
长期中,通货膨胀对失业( )。
A.(A) 有影响
B.(B) 基本没有影响
C.(C) 有很大影响
D.(D) 一点没有影响
正确答案
B
解析
暂无解析
已知等比数列


16.求
17.若



正确答案
解析
【解析】
由题意,得


考查方向
解题思路
解题步骤如下:1、根据等比数列的通项公式化简等式







易错点
本题在求等比数列的公比或求数列


正确答案
解析
【解析】


考查方向
解题思路
解题步骤如下:1、根据等比数列的通项公式化简等式







易错点
本题在求等比数列的公比或求数列


设a1,a2,a3.a4是各项为正数且公差为d(d≠0)的等差数列.
27.证明:2



28.是否存在a1,d,使得a1,a22,a33,a44依次构成等比数列?并说明理由;
29.是否存在a1,d及正整数n,k,使得a1n,a2n+k,a3n+2k,a4n+3k依次构成等比数列?并说明理由.
正确答案
(1)证明:∵

∴2



解析
(1)证明:∵

∴2



考查方向
解题思路
根据等比数列和等差数列的定义即可证明;
易错点
本题在应用定义证明过程中易错.
正确答案
不存在a1,d,使得a1,a22,a33,a44依次构成等比数列.
解析
(2)令a1+d=a,则a1,a2,a3,a4分别为a﹣d,a,a+d,a+2d(a>d,a>﹣2d,d≠0)
假设存在a1,d使得a1,a22,a33,a44依次构成等比数列,
则a4=(a﹣d)(a+d)3,且(a+d)6=a2(a+2d)4,
令t=

化简得t3+2t2﹣2=0(*),且t2=t+1,将t2=t+1代入(*)式,
t(t+1)+2(t+1)﹣2=t2+3t=t+1+3t=4t+1=0,则t=﹣
显然t=﹣
因此不存在a1,d,使得a1,a22,a33,a44依次构成等比数列.
考查方向
解题思路
(2)利用反证法,假设存在a1,d使得a1,a22,a33,a44依次构成等比数列,推出矛盾,否定假设,得到结论;
易错点
本题主要考查等差数列、等比数列的定义和性质,函数与方程等基础知识,在应用反证法过程中易错.
正确答案
不存在a1,d及正整数n,k,使得a1n,a2n+k,a3n+2k,a4n+3k依次构成等比数列
解析
(3)假设存在a1,d及正整数n,k,使得a1n,a2n+k,a3n+2k,a4n+3k依次构成等比数列,
则a1n(a1+2d)n+2k=(a1+2d)2(n+k),且(a1+d)n+k(a1+3d)n+3k=(a1+2d)2(n+2k),
分别在两个等式的两边同除以=a12(n+k),a12(n+2k),并令t=

则(1+2t)n+2k=(1+t)2(n+k),且(1+t)n+k(1+3t)n+3k=(1+2t)2(n+2k),
将上述两个等式取对数,得(n+2k)ln(1+2t)=2(n+k)ln(1+t),
且(n+k)ln(1+t)+(n+3k)ln(1+3t)=2(n+2k)ln(1+2t),
化简得,2k[ln(1+2t)﹣ln(1+t)]=n[2ln(1+t)﹣ln(1+2t)],
且3k[ln(1+3t)﹣ln(1+t)]=n[3ln(1+t)﹣ln(1+3t)],
再将这两式相除,化简得,
ln(1+3t)ln(1+2t)+3ln(1+2t)ln(1+t)=4ln(1+3t)ln(1+t),(**)
令g(t)=4ln(1+3t)ln(1+t)﹣ln(1+3t)ln(1+2t)+3ln(1+2t)ln(1+t),
则g′(t)=
令φ(t)=(1+3t)2ln(1+3t)﹣3(1+2t)2ln(1+2t)+3(1+t)2ln(1+t),
则φ′(t)=6[(1+3t)ln(1+3t)﹣2(1+2t)ln(1+2t)+3(1+t)ln(1+t)],
令φ1(t)=φ′(t),则φ1′(t)=6[3ln(1+3t)﹣4ln(1+2t)+ln(1+t)],
令φ2(t)=φ1′(t),则φ2′(t)=
由g(0)=φ(0)=φ1(0)=φ2(0)=0,φ2′(t)>0,
知g(t),φ(t),φ1(t),φ2(t)在(﹣
故g(t)只有唯一的零点t=0,即方程(**)只有唯一解t=0,故假设不成立,
所以不存在a1,d及正整数n,k,使得a1n,a2n+k,a3n+2k,a4n+3k依次构成等比数列
考查方向
解题思路
(3)利用反证法,假设存在a1,d及正整数n,k,使得a1n,a2n+k,a3n+2k,a4n+3k依次构成等比数列,得到a1n(a1+2d)n+2k=(a1+2d)2(n+k),且(a1+d)n+k(a1+3d)n+3k=(a1+2d)2(n+2k),利用等式以及对数的性质化简整理得到ln(1+3t)ln(1+2t)+3ln(1+2t)ln(1+t)=4ln(1+3t)ln(1+t),(**),多次构造函数,多次求导,利用零点存在定理,推出假设不成立.
易错点
本题主要考查等差数列、等比数列的定义和性质,在应用反正法,零点存在性定理过程中易错.
根据破产法律制度的规定,下列各项中,属于债权人会议职权的有( )。
A.决定成立清算组
B.监督清算组的清算活动
C.决定是否通过和解方案
D.监督和解程序依法进行
正确答案
B,C,D
解析
[解析] 根据《破产法》规定,债权人会议的职权主要有:(1)审查有关债权的证明材料,确认债权有无财产担保及其数额;(2)决定是否通过和解协议草案;(3)讨论通过破产财产的处理和分配方案。此外,债权人会议还有监督清算组清算活动、监督和解与整顿程序依法进行等职权。但在人民法院进入破产程序后,债权人会议无权否决人民法院关于企业破产案件的裁定。
已知各项均不为0的等差数列







17.求数列

18.设



正确答案
则

解析
则

考查方向
求数列的通项公式
解题思路
根据已知条件建立方程关系,通过求解基本量求数列通项。
易错点
注意数列类别的判定,能够根据数列的等量关系正确运算基本量
教师点评
正确列出等量关系,能够准确运算基本量是解题关键
正确答案

则
解析

则
考查方向
错位相减求和
解题思路
先根据通项写出数列,然后应用错位相减法求和
易错点
(1)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式.(2)公比q为参数时要分q=1和q≠1讨论.
教师点评
注意表达式的“错项对齐”,错位后共有n+1项,∴中间n-1项是等比数列求和.
证券投资基金按收益凭证是否可赎回,可分为开放式基金与封闭式基金。下列关于两者的区别,说法正确的是( )。
A.基金的分红方式不同
B.基金的信息披露不同
C.基金的法律依据不同
D.基金投资者地位不同
E.基金的投资目标不同
正确答案
A,B
解析
[解析] CD两项为公司型基金和契约型基金的不同;E项为成长型基金、收入型基金和平衡型基金的不同。
与理财顾问服务相比,综合理财服务的特点体现在( )。
A.综合理财服务分为理财计划和私人银行业务两类
B.综合理财服务更强调个性化的服务
C.投资收益与风险由客户或客户与银行按照约定方式获取或承担
D.综合理财服务活动中是客户授权银行代表客户按合同约定的投资方式和方向,进行投资和资产管理
E.私人银行业务是商业银行针对特定目标客户群体进行的个人理财服务
正确答案
A,B,C,D,E
解析
[解析] 本题考查综合理财服务的特点,题目所给选项说法都是正确的。
扫码查看完整答案与解析