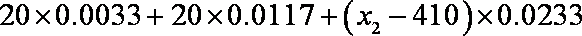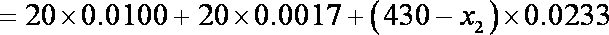- 概率与统计
- 共1335题
把正奇数依次按第一个括号1个数,第二个括号2个数,第三个括号3个数,第四个括号1
个数,……如此循环为(1),(3,5),(7,9,11),(13),(15,17),(19,21,23),……。则2015这个奇数在第 个括号内。
正确答案
504
解析
略
知识点
运行如图所示的流程图,如果输入

正确答案
9
解析
略
知识点
某商场为了了解顾客的购物信息,随机的在商场收集了100位顾客购物的相关数据,整理如下:
统计结果显示100位顾客中购物款不低于100元的顾客占60%,据统计该商场每日大约有5000名顾客,为了增加商场销售额度,对一次性购物不低于100元的顾客发放纪念品(每人一件)。(注:视频率为概率)
(1)试确定m,n的值,并估计该商场每日应准备纪念品的数量;
(2)为了迎接店庆,商场进行让利活动,一次购物款200元及以上的一次返利30元;一次性购物款小于200元的按购物款的百分比返利,具体见下表:
请估计该商场日均让利多少元?
正确答案
(1)m=20,n=20;3000(2)52000
解析
解析:(1)由已知,100位顾客中购物款不低于100元的顾客有


该商场每日应准备纪念品的数量大约为 
(2)设购物款为
当

当

当

当

所以估计日均让利为
…………10分

知识点
设


正确答案
解析
略
知识点
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示。
(1)根据图中的数据信息,求出众数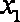
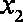
(2)小明的父亲上班离家的时间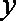

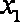
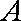
正确答案
见解析
解析
(1)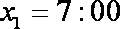
由频率分布直方图可知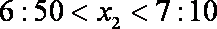
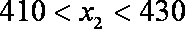
∴
解得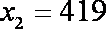
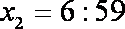
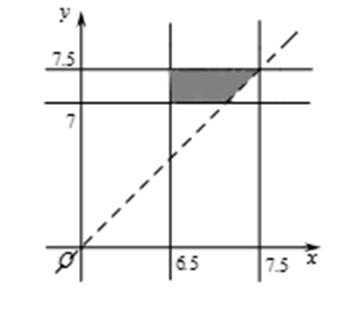
设报纸送达时间为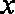
则小明父亲上班前能取到报纸等价于
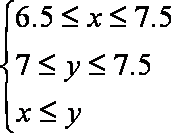
如图可知,所求概率为
知识点
某工厂生产的产品






(1)求

(2)现用分层抽样法从直径位于区间

正确答案
见解析
解析
(1) 由频率分布直方图可知

直径位于区间









(2)由频率分布直方图可知直径位于区间



























所以所求概率为
知识点
2012年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类: 第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时)。 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示。
(1) 求该小区居民用电量的中位数与平均数;
(2) 本月份该小区没有第三类的用电户出现,为鼓励居民节约用电,供电部门决定:对第一类每户奖励20元钱,第二类每户奖励5元钱,求每户居民获得奖励的平均值;
(3) 利用分层抽样的方法从该小区内选出5户居民代表,若从该5户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率。
正确答案
(1)中位数:155,平均数:156.8(2)17元(3)
解析
(1) 因为在频率分布直方图上,中位数的两边面积相等,可得中位数为155. (2分)
平均数为 
(2)
(3)由题可知,利用分层抽样取出的5户居民中属于第一类的有4户,编为


















知识点
某城市持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一,为此该城市实施了机动车尾号限行政策。现有家报社想调查了解该市区公民对“车辆限行”的态度,并在该城市里随机抽查了50人,将调查情况进行整理后制成下表:
(1)请估计该市公民对“车辆限行”的支持率(答案用百分比表示);
(2)若从年龄在[15,25),[25,35)的被调查者中采用分层抽样选取3人进行跟踪调查,求选取的3人中有2人不支持“车辆限行”的概率。
正确答案
见解析
解析
解:(1)由表中可得支持率是
(2)在[15,25),[25,35)的被调查者中的六人编号:
把[15,25)中的两人编号:1号为不支持,2号为支持;
把[25,35)中的四人编号:3号为支持,4号为支持,5号为支持,6号为不支持。
利用分层抽样则应该在[15,25)、[25,35)分别抽取1人、2人,则所有可能如下:
(1,3,4),(1,3,5),(1,3,6),(1,4,5),(1,4,6),(1,5,6)
(2,3,4),(2,3,5),(2,3,6),(2,4,5),(2,4,6),(2,5,6)
以上共有12种情形,其中有2人不支持的有3种情形,
所以选取的3人中有2人不支持“车辆限行”的概率为
知识点
从2名男生和2名女生中,任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
正确答案
解析
由题意知本题是一个古典概型,
试验包含的所有事件是从4个人安排两人,总共有C42A22=12种。
其中期六安排一名男生、星期日安排一名女生,总共有C21C21=4种,
∴其中至少有1名女生的概率P=
知识点
合肥市环保总站对2013年11月合肥市空气质量指数发布如图趋势图,
(1)请根据如图所示趋势图,完成表并根据表画出频率分布直方图,
(2)试根据频率分布直方图估计合肥市11月份AQI指数的平均值。
正确答案
见解析。
解析
(1)根据趋势图可得:
根据小矩形的高=
(2)合肥市11月份AQI指数的平均值




知识点
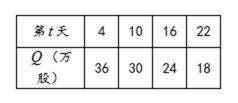
某上市股票在30天内每股的交易价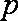
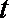
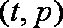
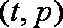
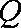
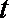
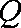
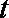
(1)根据提供的图像和表格,写出该种股票每股交易价格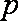
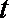
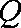
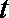
(2)用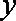
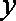
图(1):
表(1):
正确答案
见解析
解析
(1)依题意可得,每股交易价格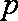
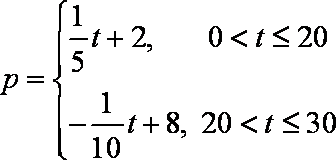
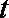
日交易量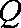
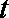
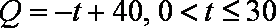
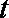
(2)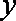
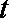
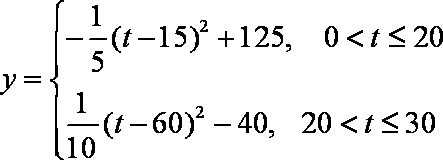
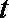
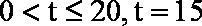
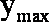
当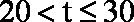
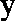

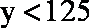
综上所述,第15天日交易额最大,最大值为125万元, (14分)
知识点
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取

(1)估计所抽取的数学成绩的众数;
(2)用分层抽样的方法在成绩为


正确答案
见解析
解析
(1)由频率分布直方图可知:样本的众数为75.………………3分
(2)由频率分布直方图可得:第三组

所以



第五组

用分层抽样的方法抽取5份得:
第四组

第五组

记抽到第四组





其中分数在



知识点
文科班某同学参加吉林省学业水平测试,物理、化学、生物获得等级









(1)试列举该同学这次水平测试中物理、化学、生物成绩是否为


(2)求该同学参加这次水平测试中恰好获得两个
(3)试设计一个关于该同学参加这次水平测试物理、化学、生物成绩情况的事件,使该事件的概率大于
正确答案
见解析。
解析
(1)该同学这次水平测试中物理、化学、生物成绩是否为

分别为







(2)由(1)可知,恰有两个A的情况为



(3)方案一:该同学参加这次水平测试中物理、化学、生物成绩不全为

理由如下:该同学参加这次水平测试中物理、化学、生物成绩不全为








方案二:该同学参加这次水平测试中物理、化学、生物成绩至少一个

理由如下:该同学参加这次水平测试中物理、化学、生物成绩不全为








知识点
(本题满分12分)为了调查某大学学生在周日上网的时间,随机对

表1:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(1)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(2)完成表3的
(3)从表3的男生中“上网时间少于60分钟”和“上网时间不少于60分钟”的人数中用分层抽样的方法抽取一个容量为5的样本,再从中任取两人,求至少有一人上网时间超过60分钟的概率。
表3 :
附:
正确答案
见解析
解析
解析:(1)设估计上网时间不少于60分钟的人数
依据题意有

所以估计其中上网时间不少于60分钟的人数是225人
(2)根据题目所给数据得到如下列联表:
其中
因此,没有90%的把握认为“学生周日上网时间与性别有关”
(3)因为上网时间少于60分钟与上网时间不少于60分钟的人数之比为












其中“至少有一人上网时间超过60分钟”包含了7种, 
知识点
某单位开展岗前培训,期间,甲、乙2人参加了5次考试,成绩统计如下:
(1)根据有关统计知识,回答问题:若从甲、乙2人中选出1人上岗,你认为选谁合适,请说明理由;
(2)根据有关概率知识,解答以下问题:
①从甲、乙2人的成绩中各随机抽取一个,设抽到甲的成绩为x,抽到乙的成绩为y,用A表示满足条件|x﹣y|≤2的事件,求事件A的概率;
②若一次考试两人成绩之差的绝对值不超过3分,则称该次考试两人“水平相当”,由上述5次成绩统计,任意抽查两次考试,求至少有一次考试两人“水平相当”的概率。
正确答案
见解析
解析
(1)甲的平均成绩为 



故甲乙二人的平均水平一样。
甲的成绩的方差为 





(2)①从甲、乙2人的成绩中各随机抽取一个,设抽到甲的成绩为x,抽到乙的成绩为y,则所有的(x,y)共有5×5=25个,
其中,满足条件|x﹣y|≤2的有(82,80)、(82,80)、(79,80)、(95,95)、(87,85),共有5个,
故所求事件的概率等于 

②从5此考试的成绩中,任意取出2此,所有的基本事件有 
其中,满足至少有一次考试两人“水平相当”的有7个:(79,80)和(87,85)、(79,80)和(82,95)、(79,80)和(87,75)、
(79,80)和(95,90)、(87,85)和(82,95)、(87,85)和(82,75)、(87,85)和(95,90),共有7个,
故所求事件的概率等于 
知识点
扫码查看完整答案与解析