- 概率与统计
- 共1335题
19.从陕西某高校男生中随机抽取
(1)求
(2)按表1的身高组别进行分层抽样, 从这






正确答案
(1)


(2)
解析
(1)解:由
由

由

(2)解:依据分层抽样的方法,抽取的



而身高在区间


记“这



从身高不低于







事件






∴
知识点
16.某市甲、乙两社区联合举行迎“五一”文艺汇演,甲、乙两社区各有跳舞、笛子演奏、唱歌三个表演项目,其中甲社区表演队中表演跳舞的有1人,表演笛子演奏的有2人,表演唱歌的有3人.
(1)若从甲、乙社区各选一个表演项目,求选出的两个表演项目相同的概率;
(2)若从甲社区表演队中选2人表演节目,求至少有一位表演笛子演奏的概率.
正确答案
(1)
(2)
解析
(1)记甲、乙两社区的表演项目:跳舞、笛子演奏、唱歌分别为A1,B1,C1;A2,B2,C2
则从甲、乙社区各选一个表演项目的基本事件有(A1,A2),(A1,B2),(A1,C2),(B1,A2),(B1,B2),(B1,C2),(C1,A2),(C1,B2),(C1,C2)共9种,
其中选出的两个表演项目相同的事件3种,所以
(2)记甲社区表演队中表演跳舞的、表演笛子演奏、表演唱歌的分别为a1,b1,b2,c1,c2,c3
则从甲社区表演队中选2人的基本事件有(a1,b1),(a1,b2),(a1,c1),(a1,c2),(a1,c3),(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),(c1,c2),(c1,c3),(c2,c3)共15种
其中至少有一位表演笛子演奏的事件有9种,所以
知识点
15. 编号分别为

(1)将得分在对应区间内的人数填入相应的空格:
(2)从得分在区间

①用运动员编号列出所有可能的抽取结果;
②求这

正确答案
见解析
解析
(1)
(2)①得分在区间






从得分在区间
















共
②记“从得分在区间




这







所以
知识点
3.若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为( )
正确答案
解析
略
知识点
4.在平面直角坐标系中,从下列五个点:A(0,0),B(2,0),C(1,1),D(0,2),(2,2)中任取三个,这三点能构成三角形的概率是( )
正确答案
解析
从5个点中取3个点,列举得ABC,ABD,ABE,ACD,ACE,ADE,BCD,BCE,BDE,CDE共有10个基本事件,而其中ACE, BCD两种情况三点共线,其余8个均符合题意,故能构成三角形的概率为
知识点
19.在某学校组织的一次篮球总投篮训练中,规定每人最多投3次;在








(1)求
(2)求随机变量

(3)试比较该同学选择在
正确答案
见解析。
解析
(1)由题设知,“

(2)根据题意
因此
(3)用




则

即该同学选择都在


知识点
18.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的部分直方图如图所示.
(1)请补全直方图,并求出轻度拥堵、中度拥堵、严重拥堵路段各有多少个;
(2)用分层抽样的方法从交通指数在[4,6),[6,8),[8,10]的路段中共抽取6个路段,求依次抽取的三个级别路段的个数;
(3)从(2)中抽出的6个路段中任取2个,求至少1个路段为轻度拥堵的概率.
正确答案
见解析。
解析
(1)补全直方图如图:
由直方图可知:(0.1+0.2)×1×20=6,
(0.25+0.2)×1×20=9,
(0.1+0.05)×1×20=3.
∴这20个路段中,轻度拥堵、中度拥堵、严重拥堵的路段分别为6个、9个、3个.
(2)由(1)知拥堵路段共有6+9+3=18个,按分层抽样从18个路段中选出6个,每种情况分别为:


(3)记(2)中选取的2个轻度拥堵路段为A1,A2,选取的3个中度拥堵路段为B1,B2,B3,选取的1个严重拥堵路段为C1,
则从6个路段选取2个路段的可能情况如下:
(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2,B2),(A2,B3),(A2,C1),(B1,B2),(B1,B3),(B1,C1),(B2,B3),(B2,C1),(B3,C1),共15种可能.
其中至少有1个轻度拥堵的有:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2,B2),(A2,B3),(A2,C1),共9种可能.
∴所选2个路段中至少1个路段轻度拥堵的概率为
知识点
6.在一个袋子中装有分别标注数字1,2,3,4,5的5个小球,这些小球除标注数字外完全相同.现从中随机取2个小球,则取出的小球标注的数字之和为3或6的概率是__________.
正确答案
解析
基本事件为(1,2)(1,3)(1,4)(1,5)(2,3)(2,4)(2,5)(3,4)(3,5)(4,5),其中和为3或6的有3个,因而有P=
知识点
17. 某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过4小时.
(1)若甲停车1小时以上且不超过2小时的概率为

(2)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为36元的概率.
正确答案
见解析
解析
解:(1)设“甲临时停车付费恰为6元”为事件A,
则 
所以甲临时停车付费恰为6元的概率是
(2)设甲停车付费a元,乙停车付费b元,其中a,b=6,14,22,30.
则甲、乙二人的停车费用构成的基本事件空间为:(6,6),(6,14),(6,22),(6,30),(14,6),(14,14),(14,22),(14,30),(22,6),(22,14),(22,22),(22,30),(30,6),(30,14),(30,22),(30,30),共16种情形.
其中,(6,30),(14,22),(22,14),(30,6)这4种情形符合题意.
故“甲、乙二人停车付费之和为36元”的概率为
知识点
14.在长为12cm的线段AB上任取一点C,现作一矩形,使邻边长分别等于线段AC、CB的长,则该矩形面积大于20cm2的概率为 。
正确答案
解析
设AC=x,则BC=12﹣x
矩形的面积S=x(12﹣x)>20
∴x2﹣12x+20<0
∴2<x<10;由几何概率的求解公式可得,矩形面积大于20cm2的概率P=

故答案为:
知识点
15.在区间[0,1]上随意选择两个实数x,y,则使
正确答案
解析
略。
知识点
17.为了解甲、乙两种品牌手机的电池充满电后的待机时间(假设都在24~96小时范围内),从这两种手机的电池中分别随机抽取100个进行测试,结果统计如下表.
(1)估计甲品牌手机的电池充满电后的待机时间小于48小时的概率;
(2)这两种品牌的手机的电池充满电后,某个电池已使用了48小时,试估计该电池是甲品牌手机的电池的概率;
(3)由于两种品牌的手机的某些差异,普遍认为甲品牌手机比乙品牌手机更显“低调”,销售商随机调查了110名购买者,并将有关数据整理为不完整的2×2列联表,写出表中A、B、C、D、E的值,并判断是否有99%的把握认为喜欢“低调型”手机与消费者的年龄有关?
附:K2=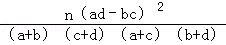
正确答案
见解析。
解析
(1)甲品牌手机的电池充满电后的待机时间小于48小时的频数是20,共有100个,
所以,甲品牌手机的电池充满电后的待机时间小于48小时的概率
(2)两种品牌的手机的电池充满电后,可以使用48小时分别是80个和60个,所以,某个电池已使用了48小时,该电池是甲品牌手机的电池的概率
(3)A=20,B=50,C=80,D=30,E=110,H0:假设是否喜欢“低调型”手机与消费者的年龄无关,根据列联表可得: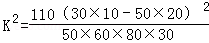
知识点
4.交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查。假设四个社区驾驶员的总人数为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)在本次训练中,从两班中分别任选一个同学,比较两人的投中次数,求甲班同学投中次数高于乙班同学投中次数的概率。
正确答案
见解析。
解析
(1)两个班数据的平均值都为7,
甲班的方差
乙班的方差
因为
(2)甲班1到5号记作



将“甲班同学投中次数高于乙班同学投中次数”记作
则

所以甲班同学投中次数高于乙班同学投中次数的概率为
知识点
3.一篮球运动员投篮命中的概率是


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析