- 概率与统计
- 共1335题
19.为了了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率。
正确答案
(1)由已知,抽取的学生人数为700
又由统计图知,男生抽取了40人,女生抽取了30人,故男生抽取的比例为
故估计男生的人数为
(2)由统计图知,男生身高在170~185的人数为14+13+4=31(人)
女生身高在170~185的人数为3+1=4(人)
∴ 估计该校学生身高在170~185cm的概率为
(3)样本中身高在180~190cm之间的男生共有6人,其中4人身高在180~185cm,分别设这四人为1,2,3,4;还有两人身高在185~190cm, 分别设这两人为A.B。
则从此6人中抽取两人,有(1,2)(1,3)(1,4)(1,A)(1,B)(2,3)(2,4)(2,A)(2,B)(3,4)(3,A)(3,B)(4,A)(4,B)(A,B)
共15种可能结果,每种结果是等可能的,所以试验中包含15个基本事件。
设事件T:“至少有1人身高在185~190cm之间”
则它包含(1,A)(1,B)(2,A)(2,B)(3,A)(3,B)(4,A)(4,B)(A,B)共9种基本事件, ∴
所以至少有一人身高在185~190cm之间的概率为
解析
解析已在路上飞奔,马上就到!
知识点
16.在一次百米比赛中,甲,乙等6名同学采用随机抽签的方式决定各自的跑道,跑道编号为1至6,每人一条跑道
(Ⅰ)求甲在1或2跑道且乙不在5或6跑道的概率;
(Ⅱ)求甲乙之间恰好间隔两人的概率.
正确答案
没有限制条件的种数为A66=720种,
(Ⅰ)先安排甲,再安排乙,剩下的全排,故有C21C31A44=144种,
根据概率公式,故甲在1或2跑道且乙不在5或6跑道的概率P=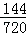
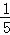
(Ⅱ)先选2人放在甲乙之间,并捆绑在一起,看作一个复合元素,再和剩下的2人全排,故有A42A22A33=144种,
根据概率公式,故甲乙之间恰好间隔两人的概率P=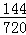
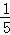
解析
解析已在路上飞奔,马上就到!
知识点
16.在一次百米比赛中,甲,乙等6名同学采用随机抽签的方式决定各自的跑道,跑道编号为1至6,每人一条跑道
(1)求甲在1或2 跑道且乙不在5或6跑道的概率 ;
(2)求甲乙之间恰好间隔两人的概率。
正确答案
(1)
(2)

)
解析
解析已在路上飞奔,马上就到!
知识点
13.从含有三件正品和一件次品的4件产品中不放回地任意取两件,则取出的两件中恰有一件次品的概率__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.执行如图的程序框图,如果输入的n是4,则输出的p是___________
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
19.从标有1,2,3,…,7的7个小球中取出一个球,记下它上面的数字,放回后再取出一个球,记下它上面的数字,然后把两球上的数字相加,求取出两球上的数字之和大于11或者能被4整除的概率。
正确答案
从标有1,2,3,…,7的7个小球中取出一个球,记下它上面的数字,放回后再取出一个球,记下它上面的数字,共有7×7=49种不同情况,
其中两球上的数字之和大于11或者能被4整除的事件有:
(1,3),(1,7),(2,2),(2,6),(3,1),(3,5),(4,4),(5,3),
(5,7),(6,2),(6,6),(7,1),(7,5),(6,7),(7,6),(7,7),共16种,
故取出两球上的数字之和大于11或者能被4整除的概率P=
解析
解析已在路上飞奔,马上就到!
知识点
17.从含有两件正品和一件次品的3件产品中,每次任取1件
(1)每次取出后不放回,连续取两次,求取出的产品中恰有一件次品的概率;
(2)每次取出后放回,连续取两次,求取出的产品中恰有一件次品的概率。
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
16.某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
B配方的频数分布表
(Ⅰ)分别估计用A配方,B配方生产的产品的优质品率;
(Ⅱ)已知用B配方生成的一件产品的利润y(单位:元)与其质量指标值t的关系式为y=
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
正确答案
(Ⅰ)由试验结果知,用A配方生产的产品中优质的频率为
∴ 用A配方生产的产品的优质品率的估计值为0.3.
由试验结果知,用B配方生产的产品中优质品的频率为
∴ 用B配方生产的产品的优质品率的估计值为0.42
(Ⅱ)用B配方生产的100件产品中,其质量指标值落入区间
[90,94),[94,102),[102,110]的频率分别为0.04,0.54,0.42,
∴ P(X=﹣2)=0.04,P(X=2)=0.54,P(X=4)=0.42,
即X的分布列为
∴ X的数学期望值EX=﹣2×0.04+2×0.54+4×0.42=2.68
解析
解析已在路上飞奔,马上就到!
知识点
20.如图所示,正五边形ABCDE的每个顶点对应着一个整数,且这五个整数的和为正数.若其3个相邻顶点对应的整数依次为x、y、z,且y<0,则要进行如下的操作:把整数x、y、z分别换为x+y,﹣y,z+y,称其为一次“求正”操作.只要五个整数中有负整数,“求正”操作就要继续进行.
(Ⅰ)若 A,B,C,D,E对应的数分别为3,﹣2,﹣2,4,1,写出每一步“求正”操作直到终止;
(Ⅱ)若 A,B,C,D,E对应的数分别为a,﹣4,5,1,2,并且经过两次“求正”操作后终止,求实数a的值;
(Ⅲ)判断对任意满足条件的数组,“求正”操作是否经过有限次后就一定能终止?说明理由.
正确答案
(I)操作依次为:3,﹣2,﹣2,4,1→1,2,﹣4,4,1,→1,﹣2,4,0,1,→
﹣1,2,2,0,1,→1,1,2,0,0.
(II)分两种情况,先对﹣4操作,过程如下:
a,﹣4,5,1,2→a﹣4,4,1,1,2.此时,a﹣4必为负数,继续操作,→4﹣a,a,1,1,a﹣2.
于是有
若对a进行操作,a,﹣4,5,1,2→﹣a,a﹣4,5,1,a+2.此时a﹣4<a﹣2,
故可对a﹣4进行操作,﹣a,a﹣4,5,1,a+2→﹣4,4﹣a,a+1,1,a+2.显然无法终止,不符合题意.
综上,所求a的值为2或3.
(III)为方便见,我们把5个数的环列写成横我v,w,x,y,z.不妨设y<0,经变换后得v,w,x+y,﹣y,z+y.
考察5个数的平方和再加上每相邻两数和的平方这一整体,那么变换前后的差是:
{v2+w2+(x+y)2+(﹣y)2+(z+y)2+(v+w)2+(w+x+y)2+x2+z2+(z+y+v)2]﹣{v2+w2+(x+y)2+y2+(z+y)2+(v+w)2+(w+x)2+x2+z2+(z+v)2]=2y(v+w+x+y+z)<0,
由此可得,这一整体每经过一次变换都要减小,但最初这一整体是正整数,经变换后还是正整数,
而正整数是不能无限减小的,所以变换必定有终止的时候.
即“求正”操作经过有限次后就一定能终止.
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)从区间





(2)若连续掷两次骰子(骰子六个面上标注的点数分别为






正确答案
(1)




即

(2)由已知:
所以
即




当


当


当


满足

而基本事件总数为

解析
解析已在路上飞奔,马上就到!
知识点
8.将3名学生安排到


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:
(Ⅰ)求图中

(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取5名参加中心广场的宣传活动,再从这5名中采用简单随机抽样方法选取3名志愿者担任主要负责人,求这3名志愿者中“年龄低于35岁”的人数大于1的概率。
正确答案
(I)∵小矩形的面积等于频率,
∴除
500名志愿者中,年龄在

(II)用分层抽样的方法,从中选取5名,则其中年龄“低于35岁”的人有3名,“年龄不低于35岁”的人有2名.
由列举法可得,总共为20种,
符合条件的为14种,概率为
解析
解析已在路上飞奔,马上就到!
知识点
11.已知某商
正确答案
1211
解析
解析已在路上飞奔,马上就到!
知识点
10.袋中装有同样大小的




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 为预防
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知
正确答案
(1)
即

(2)C组样本个数为y+z=2000-(673+77+660+90)=500,
现
(3)设测试不能通过事件为A ,C组疫苗有效与无效的可能的情况记为(y,z) 由(2)知 

(465,35)、(466,34)、(467,33)、……(475,25)共11个
若测试不能通过,则77+90+z>200,即z>33
事件A包含的基本事件有:((465,35)、(466,34)共2个


解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析

































