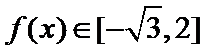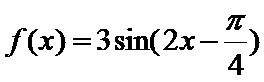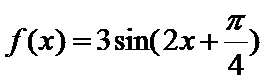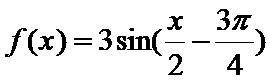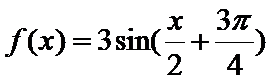- 由y=Asin(ωx+φ)的部分图象确定其解析式
- 共50题
函数
正确答案
知识点
3.函数
正确答案
知识点
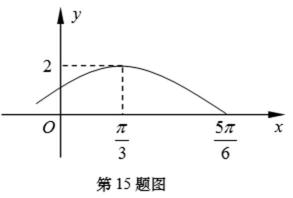
15.设函数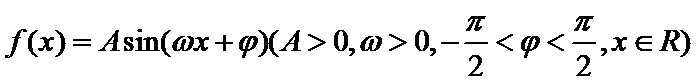
(1)求函数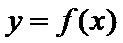
(2)当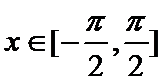
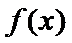
正确答案
(1)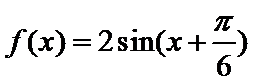
(2)
解析
试题分析:本题属于三角函数图像的基本问题,题目的难度是逐渐由易到难,(1)直接按照求A、ω、φ步骤来求(2)转化成求函数的最值,要结合图像,要特别注意函数的定义域。
(1)由图象知,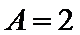
又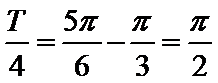
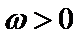
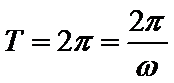
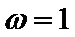
所以
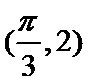
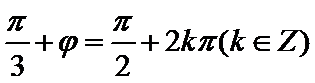
即
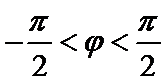
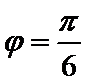
所以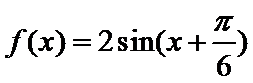
(2)当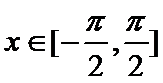
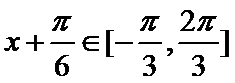
所以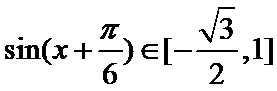
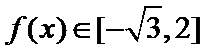
考查方向
解题思路
本题考查三角函数的图形和性质,解题步骤如下:
1、根据函数图像,确定A、ω、φ,进而求出函数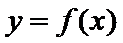
2、求函数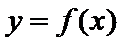
易错点
1、第一问中的根据角的范围如何确定φ。2、第二问中求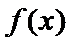
知识点
8.函数f(x)=
正确答案
知识点
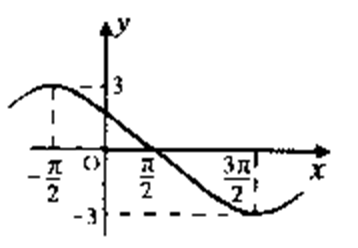
7.函数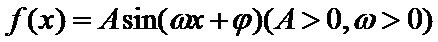
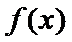
为( )
正确答案
解析
由图可知周期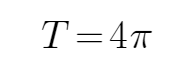
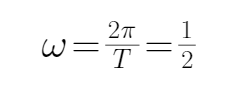
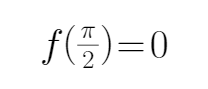
即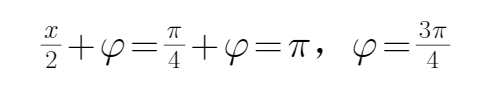
考查方向
三角函数的图象与性质
解题思路
根据图象,求解参数的值,进而求出解析式
易错点
求参数错误,数形结合思想运用不恰当
知识点
13.已知函数




正确答案
解析
由题意可知
又∵函数为偶函数 ∴
又∵
考查方向
解题思路
1、根据正弦型函数的图像容易得到




易错点
本题易于在求解
知识点



正确答案
解析
由题意可知T=



考查方向
解题思路
1、利用相邻的零点与对称轴之间的距离求出


易错点
本题易于在求解
知识点
17.已知向量





(I)求
(II)求函数
(III)若

正确答案
(1)
(2)增区间[

(3)
解析
本题属于三角函数应用中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求,
(2)对函数进行变形,转化成可用已知函数表示的形式,最后代入求值。
解:(I)f(x)=2



























考查方向
本题考查了向量的乘法、正(余)弦的二倍角、函数的单调区间、三角的恒等变形与化简求值等知识点,属于中档题,也是高考必考题型之一。向量的坐标式、向量的平行与垂直、三角函数的单调性、周期性、对称轴等知识常常会结合在一起进行命题。
易错点
1、二倍角的余弦公式中符号搞错
2、第(III)问的变形化简会出错
知识点
10. 函数



正确答案
解析
由图可知,A=1,





∴则
考查方向
本题主要考查了图形变换
解题思路
先通过图象得出函数解析式
易错点
(1)利用y=Asin(ωx+φ)的图象特征,求出函数y=Asin(ωx+φ)的解析式,
(2)根据y=Asin(ωx+φ)的图象变换规律及正弦函数的图象和性质,求得m的最小值.
知识点
8.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析