- 线性回归方程
- 共29题
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费



22.根据散点图判断,

23.根据(I)的判断结果及表中数据,建立y关于x的回归方程;
24.已知这种产品的年利润z与x,y的关系为
(i)当年宣传费
(ii)当年宣传费
附:对于一组数据




正确答案
(Ⅰ)


解析
(Ⅰ)由散点图可以判断,


考查方向
解题思路
试题分析:(Ⅰ)由散点图及所给函数图像即可选出适合作为拟合的函数;
易错点
本题在寻求拟合函数比较易错
正确答案
(Ⅱ)
解析
(Ⅱ)令




∴
∴


∴


考查方向
易错点
在非线性回归方程进行预报预测;应用易错.
正确答案
(Ⅲ)46.24
解析
(Ⅲ)(ⅰ)由(Ⅱ)知,当



(ⅱ)根据(Ⅱ)的结果知,年利润z的预报值

∴当



故宣传费用为46.24千元时,年利润的预报值最大.……12分
考查方向
解题思路
(Ⅲ)(ⅰ)利用



易错点
在非线性回归方程进行预报预测;应用易错.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费

表中w1 =


21.根据散点图判断,y=a+bx与y=c+d
22.根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
23.以知这种产品的年利率z与x、y的关系为z=0.2y-x。根据(Ⅱ)的结果回答下列问题:
(i) 年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii) 年宣传费x为何值时,年利率的预报值最大?
附:对于一组数据(u1 v1),(u2 v2)…….. (un vn),其回归线v=
正确答案
正确答案
正确答案
PM2.5是指空气中直径小于或等于2.5微米的颗粒物,为了探究车流辆与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的浓度的数据如下表:
19.根据上表数据,用最小二乘法求出

20.若周六同一时间段车流量是200万辆,试根据19题中求出的线性回归方程预测,此时PM2.5的浓度是多少?
附:线性回归方程




正确答案

解析
试题分析:本题属于最小二乘法、回归直线方程的求法、线性回归分析,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:






故


考查方向
解题思路
直接利用公式进行计算;
易错点
相关知识点不熟容易处错。
正确答案

解析
试题分析:本题属于最小二乘法、回归直线方程的求法、线性回归分析,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:当


考查方向
解题思路
根据回归直线方程进行估计.
易错点
相关知识点不熟容易处错。
3.根据如下样本数据

正确答案
解析
画出散点图,可知>0,<0 ,所以选B
考查方向
解题思路
画出散点图,可知>0,<0
易错点
不理解数据与回归直线的关系而出错
知识点
下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图
19.由折线图看出,可用线
20.建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:


参考公式:相关系数
回归方程
正确答案
(Ⅰ)





解析
(I)由折线图中数据和附注中参考数据得



因为y与t的相关系数近似为0.99,说明y与t的线性相关程度相当高,从而可以用线性回归模型拟合y与t的关系
考查方向
解题思路
(I)根据相关系数r公式求出相关数据后,然后代入公式即可求得r的值,最后根据其值大小回答即可;
易错点
对线性相关与线性回归方程的求法与应用理解出现错误、计算错误
正确答案
(Ⅱ)1.82亿吨
解析
(Ⅱ)由


所以,

将2016年对应的

所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.
考查方向
解题思路
(II)利用最小乘法的原理提供的回归方程,准确求得相关数据即可建立y关于t的回归方程,然后作预测。
易错点
对线性相关与线性回归方程的求法与应用理解出现错误、计算错误
5.某工厂对新研发的一种产品进行试销,得到如下数据表:
根据上表可得回归直线方程


正确答案
解析
由表格知


考查方向
解题思路
通过表格算出

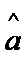
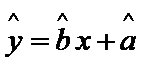
易错点
x,y任取某组给定值代入计算
知识点
5.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了4次试验,收集数据如表示:根据右表可得回归方程

正确答案
解析
由题中给出的表格得





考查方向
解题思路
1.先求出样本点的中心

易错点
1.不知道回归直线过样本点的中心,误将表格中的点带入回归直线导致出错2.运算结果出错。
知识点
3. 某考察团对全国10大城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)统计调查,y与x具有相关关系,回归方程
正确答案
解析
考查方向
解题思路
直接代入回归方程, 可求得
易错点
不知道样本中心与线性回归直线的关系,题意理解不清
知识点
某汽车公司为调查4S店个数对该
19.根据该统计数据进行分析,求y关于x的线性回归方程;
20.现要从A,B,E三座城市的9家4S店中选取4家做深入调查,求A城市中
被选中的4S店个数X的分布列和期望.
附:回归直线的斜率和截距的最小二乘法估计公式分
, .
正确答案
(1)
解析
(Ⅰ)




考查方向
解题思路
带公式求线性回归方程;
先找出随机变量的所有取值,分别求对应的概率并列出表格,然后到公式求出期望。
易错点
带公式求方程计算出错
分布列中随机变量求值及其概率求错
正确答案
(2)
解析






-------------9分

考查方向
解题思路
带公式求线性回归方程;
先找出随机变量的所有取值,分别求对应的概率并列出表格,然后到公式求出期望。
易错点
带公式求方程计算出错
分布列中随机变量求值及其概率求错
正确答案
知识点
扫码查看完整答案与解析




































