- 算法
- 共608题
19.衡水市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下:
(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为
求甲在初赛中答题个数的分布列及数学期望.
正确答案
(I)获得参赛资格的人数
(II)平均成绩:
(III)设甲答对每一道题的概率为.P
则

解析
解析已在路上飞奔,马上就到!
知识点
1.下列语句中是算法的个数为( )
①从济南到巴黎:先从济南坐火车到北京,再坐飞机到巴黎;
②统筹法中“烧水泡茶”的故事;
③测量某棵树的高度,判断其是否是大树;
④已知三角形的一部分边长和角,借助正余弦定理求得剩余的边角,再利用三角形的面积公式求出该三角形的面积。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.程序框图如下,若恰好经过
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
4.如图所示的流程图的输出S的值是( )
正确答案
20
解析
解析已在路上飞奔,马上就到!
知识点

正确答案
32
解析
解析已在路上飞奔,马上就到!
知识点
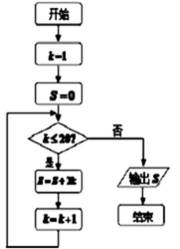
12.如果执行如图所示的程序图(判断条件k≤20?),那么输出的S=_____________。
正确答案
420
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-1:几何证明选讲
如图,已知AB是圆O的直径,C为圆O上一点,CD⊥AB于点D,弦BE与CD,AC分别交于点M,N,且MN=MC.
(1)求证:MN=MB;
(2)求证:OC⊥MN.
23.选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线



24.选修4-5:不等式选讲
已知函数
(1)若


(2)当

正确答案
22.
(1)连接AE,BC,∵AB是圆O的直径,∴∠AEB=90°,∠ACB=90°.
∵MN=MC, ∴∠MCN=∠MNC.
又∵∠ENA=∠MNC, ∴∠ENA=∠MCN,∴∠EAC=∠DCB.
∵∠EAC=∠EBC, ∴∠MBC=∠MCB,∴MB=MC. ∴MN=MB.
(2)设OC∩BE=F,∵OB=OC,∴∠OBC=∠OCB.
由(1)知,∠MBC=∠MCB,∴∠DBM=∠FCM.
又∵∠DMB=∠FMC,∴∠MDB=∠MFC
即∠MFC=90°.∴OC⊥MN.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
8.在平面直角坐标系xOy中,已知双曲线C:

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l

正确答案
解析
因为m⊥α,l⊥m,l
又因为m,n为异面直线,所以α与β相交,且l平行于它们的交线,故选D
知识点
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5,
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)证明:在线段BC1上存在点D,使得AD⊥A1B,并求
正确答案
见解析
解析
(1)因为AA1C1C为正方形,所以AA1⊥AC.
因为平面ABC⊥平面AA1C1C,且AA1垂直于这两个平面的交线AC,所以AA1⊥平面ABC.
(2)由(1)知AA1⊥AC,AA1⊥AB.
由题知AB=3,BC=5,AC=4,所以AB⊥AC.
如图,以A为原点建立空间直角坐标系A-xyz,则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4)。
设平面A1BC1的法向量为n=(x,y,z),
则
令z=3,则x=0,y=4,所以n=(0,4,3)。
同理可得,平面B1BC1的法向量为m=(3,4,0)。
所以cos〈n,m〉=
由题知二面角A1-BC1-B1为锐角,
所以二面角A1-BC1-B1的余弦值为
(3)设D(x,y,z)是直线BC1上一点,且

所以(x,y-3,z)=λ(4,-3,4)。
解得x=4λ,y=3-3λ,z=4λ.
所以
由


因为
此时,
知识点
扫码查看完整答案与解析