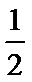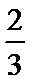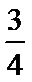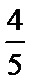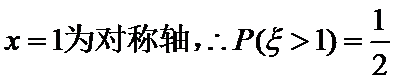- 二次函数的零点问题
- 共17题
8.已知函数f(x)=

正确答案
解析
由










考查方向
解题思路
根据函数的单调性先求出



易错点
忽略
教师点评
函数性质综合应用
知识点
14.若函数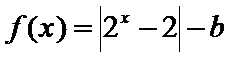
正确答案
(-2,+∞)
考查方向
易错点
1.不注意指数函数的有界性导致出错;
知识点
16.已知函数f(x)= cos2x +asinx在区间(0,n
则实数a的值为____ .
正确答案
解析
由





























考查方向
解题思路
先把函数的零点问题转化为方程的根的问题,即


易错点

知识点
11.已知函数


正确答案
解析
先根据题意作出函数的




考查方向
解题思路
1.根据函数
易错点
1。不会做函数
件:函数
知识点
2.函数f(x)=x2-
正确答案
解析
显然
若函数在区间(1,2)上有零点,则
解得-1<a<3.
所以当函数
实数a的取值范围为(-∞,-1]∪[3,+∞).
知识点
12.已知函数



正确答案
解析





又因为




考查方向
解题思路
利用正弦曲线的对称性,知道





易错点
不会作出分段函数图像,找不到对称关系。
知识点
3.设随机变量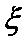
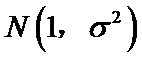
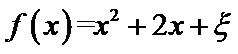
正确答案
解析
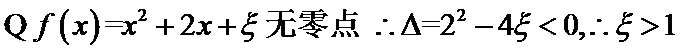
考查方向
解题思路
【解题思路】本题属于简单题,可使用直接法,
易错点
该题容易忽视正态分布曲线的对称性
知识点
已知






求数列

求数列


正确答案


解析
设等差数列


所以
设等比数列



所以
从而
考查方向
解题思路
根据a1和a4的值求出等差数列的公差,再结合等差数列的通项公式即可求出an;
设等比数列{bn-an}的公比为q,根据题意求出q,进而可得等比数列{bn-an}的通项公式,至此即可得到bn;
易错点
等差数列和等比数列基本量的计算要准确,一步计算错误会影响下面的计算结果和得分情况.
正确答案

解析
由上知
所以,数列


考查方向
解题思路
根据数列{bn}的通项公式,将其分为数列{3n}和数列{2n-1}之和,再分别根据等差数列与等比数列的前n项和公式求解即可.
易错点
等差数列和等比数列基本量的计算要准确,一步计算错误会影响下面的计算结果和得分情况.
扫码查看完整答案与解析