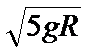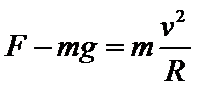- 向心力
- 共114题
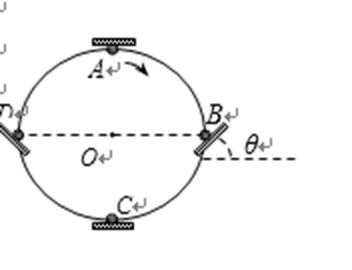
18.太极球是广大市民中较流行的一种健身器材。将太极球(拍和球)简化成如图所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做半径为R的匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势。A为圆周的最高点,C为最低点,B、D与圆心O等高。球的质量为m,重力加速度为g,则
正确答案
解析
A、设球运动的线速率为v,半径为R,则在A处时: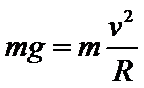
解得:F=2mg,即在C处板对球所需施加的力比A处大mg,故A错误;
B、球在运动过程中,动能不变,势能时刻变化,故机械能不守恒,故B错误;
C、球在任意时刻的速度大小相等,即球在最低点C的速度最小值为等于在最高点最小速度,根据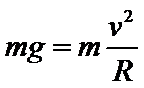
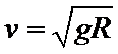
D、在B处合力提供向心力,即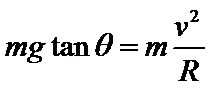
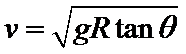
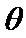
考查方向
解题思路
球在运动过程中受重力和支持力,由向心力公式可以求在各点的受力情况,并结合机械能守恒的条件分析即可。
易错点
抓住球在竖直面内始终不脱离板而做半径为R的匀速圆周运动,分析受力情况,注意合力提供小球运动的向心力。
知识点
3.一倾角为θ=37°的粗糙斜面与一光滑的半径R=0.9m的竖直圆轨道相切于P点,O 点是轨道圆心,轨道上的B点是最高点,D点是最低点,C点是最右的点,斜面上的A点与B点等高。一质量m=1.0kg的小物块在A点以沿斜面向下的初速度v0刚好能在斜面上匀速运动,通过P点处的小孔进入圆轨道并恰能做完整的圆周运动。g=10m/s2,sin37°=0.6,cos37°=0.8。则下列说法正确的是()
正确答案
解析
A、在B点,由mg=m

从P到B,由机械能守恒定律得:mgR(1+cos37°)+
解得:v0=
B、物块在斜面上做匀速运动,由平衡条件得:mgsin37°=μmgcos37°,得:μ=0.75.故B错误.
C、从D到B的过程,由机械能守恒定律得:mg•2R+
在D点,由牛顿第二定律得:FD′﹣mg=m
联立解得:FD′=6mg=60N,由牛顿第三定律知,小物块在D点时对轨道压力FD=FD′=60N.故C正确.
D、小物块在C点受到重力和轨道水平向左的弹力,其合外力斜向左下方,故D错误.
考查方向
解题思路
小球从P到B的过程,运用机械能守恒定律列式.在B点,由重力等于向心力列式,联立可求得v0.对AP段,运用平衡条件列式可求得动摩擦因数μ.根据小物块的受力情况,分析在C的合外力方向.由机械能守恒定律求出小物块经过D点的速度,再由牛顿运动定律求小物块对轨道的压力.
易错点
本题的关键要根据物块的运动过程和状态,灵活选取力学规律解答,要知道最高点的临界条件是重力等于向心力.圆周运动中求压力往往根据机械能守恒定律和向心力结合研究.
知识点
16.质量为用的小球用弹性轻绳系于O点(右上图),将其拿到与O同高的A点,弹性绳处于自然
伸长状态,此时长为l0.将小球由A点无初速度释放,当小球到达O的正下方B点
时,绳长为l小球速度为v,方向水平.则下列说法正确的是
正确答案
解析
A、小球在B点时所受合外力提供向心力,弹性绳的弹力大于重力,即有
得
B、根据牛顿第二定律得:小球在B点时所受合外力大小为
C、小球从A至B,根据动能定理得:

D、小球从A到B,弹性绳的弹力对小球做负功,小球的机械能有损失,损失的机械能等于克服弹力做的功,为
考查方向
解题思路
小球在B点时所受合外力提供向心力,弹力大于重力.由动能定理分析重力做功.由能量守恒定律分析机械能的损失。
易错点
右图中B球的机械能不守恒,只有B球和弹簧组成的系统机械能守恒.在B点,由合外力充当向心力。
知识点
24.如图所示,一质量为m的小方块(可视为质点),系在一伸直的轻绳一端,绳的另一端固定在粗糙水平面上,绳长为r。给小方块一沿垂直轻绳的初速度v0,质点将在该水平面上以绳长为半径做圆周运动,运动一周后,其速率变为
正确答案
均匀
解析
利用“化曲为直”的思想,小方块在运动一周的过程中,可以看做小方块做加速度为a=μg的匀减速直线运动,则绳的拉力为:F=



考查方向
解题思路
1.小方块做圆周运动,则小方块受到绳子的拉力提供向心力;2.利用“化曲为直”的思想,小方块在运动一周过程中,可以看做小方块做加速度为a=μg的匀减速直线运动,则v2=2ax=2μgx,又因为x=rθ,所以F=
易错点
掌握“化曲为直”的思想,小方块在运动一周过程中,可以看做小方块做加速度为a=μg的匀减速直线运动
知识点
18.图中小孩正在荡秋千,在秋千离开最高点向最低点运动的过程中,下列说法中正确的是( )
正确答案
解析
当秋千离开最高点,向最低点运动的过程中,小孩的速度增大,合外力的一个分力指向圆心,提供向心力,另一个分力沿着切线方向,使小孩速度增大所以加速度方向可能沿图中的a方向,所以C对。在向下运动过程中,速度越来越大,向心力由拉力减去重力的分量合成,所以拉力越来越大,A对B错。
考查方向
解题思路
当秋千离开最高点,向最低点运动的过程中,小孩的速度增大,加速度不沿圆心方向,据此即可选择
易错点
考查曲线运动及其相关知识,明确小孩的运动规律和受力特点
知识点
扫码查看完整答案与解析