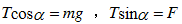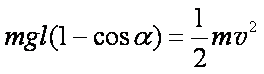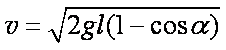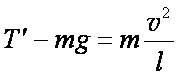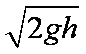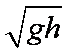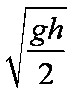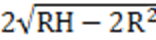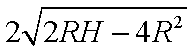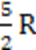- 机械能守恒定律
- 共101题
如图所示，长为L、内壁光滑的直管与水平地面成30°角固定放置。将一质量为m的小球固定在管底，用一轻质光滑细线将小球与质量为M=km的小物块相连，小物块悬挂于管口。现将小球释放，一段时间后，小物块落地静止不动，小球继续向上运动，通过管口的转向装置后做平抛运动，小球在转向过程中速率不变。(重力加速度为g)
（1）求小物块下落过程中的加速度大小；
（2）求小球从管口抛出时的速度大小；
（3）试证明小球平抛运动的水平位移总小于
正确答案
（1） 
（2）
（3）见解析
解析
（1）设细线中的张力为T，根据牛顿第二定律
且
解得：
（2）设M落地时的速度大小为v，m射出管口时速度大小为v0，M落地后m的加速度为a0。
根据牛顿第二定律
匀变速直线运动
解得： 
（3）平抛运动
解得
因为
知识点
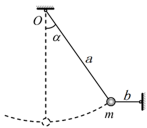
如图所示，一质量为m的小球（小球的大小可以忽略），被a、b两条轻绳悬挂在空中。已知轻绳a的长度为l，上端固定在O 点，轻绳b水平。
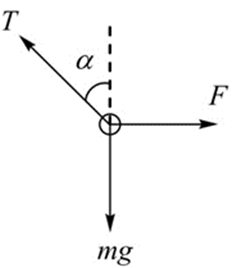
（1）若轻绳a与竖直方向的夹角为 ，小球保持静止。画出此时小球的受力图，并求轻绳b对小球的水平拉力的大小；
（2）若轻绳b突然断开，小球由图示位置无初速释放，求当小球通过最低点时的速度大小及轻绳a对小球的拉力。（不计空气阻力，重力加速度取g）
正确答案
见解析。
解析
（1）小球的受力图见上图
根据平衡条件，应满足
可得小球受到的拉力
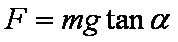
（2）释放后，小球沿圆弧运动，到达最低点，只有重力做功，由系统机械能守恒
则通过最低点时小球的速度
小球沿圆周运动，通过最低点，受重力和绳的拉力，根据牛顿第二定律
解得轻绳对小球的拉力
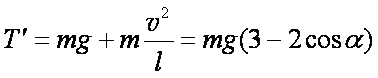
知识点
1.在同一位置以相同的速率把三个小球分别沿水平、斜向上、斜向下方向抛出，不计空气阻力，则落在同一水平地面地面时的速度大小（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
如图所示，装置的左边是足够长的光滑水平面，一轻质弹簧左端固定，右端连接着质量 M=2kg的小物块A。装置的中间是水平传送带，它与左右两边的台面等高，并能平滑对接。传送带始终以n=2m/s 的速度逆时针转动。装置的右边是一光滑的曲面，质量m=1kg的小物块B从其上距水平台面h=1.0m处由静止释放。已知物块B与传送带之间的摩擦因数 n=0.2, f=1.0m。设物块A、B中间发生的是对心弹性碰撞，第一次碰撞前物块A静止且处于平衡状态。取g=10m/s2。
（1）求物块B与物块A第
（2）一次碰撞前的速度大小；通过计算说明物块B与物块A第一次碰撞后能否运动到右边曲面上？
（3）如果物块A、B每次碰撞后，物块A再回到平衡位置时都会立即被锁定，而当他们再次碰撞前锁定被解除，试求出物块B第n次碰撞后运动的速度大小。
正确答案
（1）4 m/s
（2）不能
（3）
解析
（1）设物块B沿光滑曲面下滑到水平位置时的速度大小为v0，由机械能守恒知mgh＝
设物块B在传送带上滑动过程中因受摩擦力所产生的加速度大小为a
μmg＝ma③
设物块B通过传送带后运动速度大小为v，有
v2－v02＝－2al④
结合②③④式解得v＝4 m/s⑤
由于v＞u＝2 m/s，所以v＝4 m/s即为物块B与物块A第一次碰撞前的速度大小。
（2）设物块A、B第一次碰撞后的速度分别为V、v1，取向右为正方向，由弹性碰撞知
－mv＝mv1＋MV⑥
解得
即碰撞后物块B沿水平台面向右匀速运动。
设物块B在传送带上向右运动的最大位移为l′，则
0－v12＝－2al′⑨
所以物块B不能通过传送带运动到右边的曲面上。
（3）当物块B在传送带上向右运动的速度为零后，将会沿传送带向左加速，可以判断，物块B运动到左边台面时的速度大小为v1，继而与物块A发生第二次碰撞，设第二次碰撞后物块B速度大小为v2，同上计算可知
物块B与物块A第三次碰撞、第四次碰撞…，碰撞后物块B的速度大小依次为
则第n次碰撞后物块B的速度大小为
知识点
如图所示，质量m＝1.0 kg的物块放在倾角为θ的斜面上，从A点由静止开始释放，过B点时速度为2.0 m/s，过C点时速度为3.0 m/s.已知BD长为2.1 m，CD长为1.6 m，(g取10 m/s2)
（1）物块下滑的加速度多大？
（2）选D处为零势能面，写出物块下滑过程中最大重力势能与倾角θ的关系式。
（3）假设物块下滑过程中机械能守恒，则倾角θ是多少？
正确答案
（1）5m/s2
（2） 
（3）30°
解析
（1）从B到C过程中，x＝0.5 m(1分)
由v－v＝2ax(2分)
所以a＝5 m/s2.(1分)
（2）A点速度为零，设从A到B距离为x′
由v－02＝2ax′(2分)
得x′＝0.4 m(1分)
所以D、A之间的高度为
H＝(x′＋BD)sinθ＝2.5sinθ(2分)
最大重力势能Epm＝mgH＝25sinθ(2分)
（3）若机械能守恒，有EkB＋EpB＝EkC＋EpC
即：mgxsinθ＝
解得θ＝30°(1分)
知识点
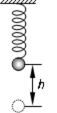
如图所示，在轻弹簧的下端悬挂一个质量为m的小球A，若将小球A从弹簧原长位置由静止释放，小球A能够下降的最大高度为h。若将小球A换为质量为2m的小球B，仍从弹簧原长位置由静止释放，则小球B下降h时的速度为（重力加速度为g，不计空气阻力。）
A
B
C
D0
正确答案
解析
略
知识点
将地面上静止的货物竖直向上吊起，货物由地面运动至最高点的过程中，
正确答案
解析
根据
知识点
由光滑细管组成的轨道如图所示，其中AB段是半径为R的四分之一圆弧，轨道固定在竖直平面内。一质量为m的小球，从距离水平地面高为H的管口D处静止释放，最后能够从A端水平抛出落到地面上。下列说法正确的是
A小球落到地面相对于A点的水平位移值为
B小球落到地面相对于A点的水平位移值为
C小球能从细管A端水平抛出的条件是H>2R
D小球能从细管A端水平抛出的最小高度Hmin=
正确答案
解析
当小球从H=2R处落下，到A点速度为0，落点距A水平距离为0；取H=4R，小球到达A处有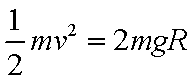
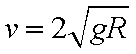
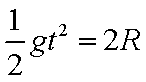
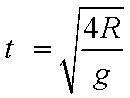
知识点
一蹦极运动员身系弹性蹦极绳从水面上方的高台下落，到最低点时距水面还有数米距离。假定空气阻力可忽略，运动员可视为质点，下列说法正确的是
正确答案
解析
运动员到达最低点过程中，重力做正功，所以重力势能始终减少， A项正确。蹦极绳张紧后的下落过程中，弹性力做负功，弹性势能增加，B 项正确。蹦极过程中，运动员、地球和蹦极绳所组成的系统，只有重力和弹性力做功，所以机械能守恒，C 项正确。重力势能的改变与重力势能零点选取无关，D 项错误。
知识点
18． “蹦极”运动中，长弹性绳的一端固定，另一端绑在人身上，人从几十米高处跳下。将蹦极过程简化为人沿竖直方向的运动。从绳恰好伸直，到人第一次下降至最低点的过程中，下列分析正确的是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析