- 机械能守恒定律
- 共101题
如图,ABC和ABD为两个光滑固定轨道,A、B、E在同一水平面上,C、D、E在同一竖直线上,D点距水平面的高度为h,C点的高度为2h,一滑块从A点以初速度v0分别沿两轨道滑行到C或D处后水平抛出。
(1)求滑块落到水平面时,落点与E点间的距离sC和sD;
(2)为实现sC<sD,v0应满足什么条件?
正确答案
(1)滑块落到水平面时,落点与E点间的距离 sC=

(2)初速度应满足

解析
(1)设抛出点高度为y,根据机械能守恒

所以平抛的初速度为 v=
平抛后物体在竖直方向上做自由落体运动,
所以落地时间t满足 y=
所以 t=
落地点离抛出点的水平距离s=vt=
分别以y=2h和y=h代入得:
sC=
sD=
(2)由题意知,要使sC<sD,
也就是要有2(v02﹣4gh)<v02﹣2gh,
所以v02<6gh,
又滑块必须能到达C点,
即 vC2=v02﹣4gh,
所以 v02>4gh,
因此初速度应满足

知识点
如图所示,圆管构成的半圆形竖直轨道固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一初速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2R。重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求:
(1)粘合后的两球从飞出轨道到落地的时间t;
(2)小球A冲进轨道时速度v的大小。
正确答案
见解析。
解析
(1)粘合后的两球飞出轨道后做平抛运动,竖直方向分运动为自由落体运动,有

解得 
(2)设球A的质量为m,碰撞前速度大小为v1,把球A冲进轨道最低点时的重力势能定为0,由机械能守恒定律知 
设碰撞后粘合在一起的两球速度大小为v2,由动量守恒定律知 
飞出轨道后做平抛运动,水平方向分运动为匀速直线运动,有 
综合②③④⑤式得
知识点
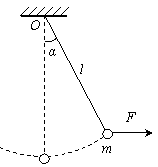
如图所示,长度为l的轻绳上端固定在O点,下端系一质量为m的小球(小球的大小可以忽略)。
在水平拉力F的作用下,轻绳与竖直方向的夹角为
由图示位置无初速度释放小球,求当小球通过最低点时的速度大小及轻绳对小球的拉力。不计空气阻力。
正确答案
见解析。
解析
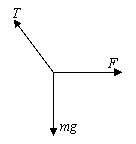
(1)受力图见图
根据平衡条件,的拉力大小F=mgtanα
(2)运动中只有重力做功,系统机械能守恒: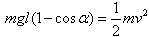
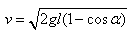
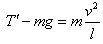
解得轻绳对小球的拉力: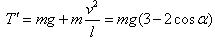
知识点
2013年我国相继完成“神十”与“天宫”对接.“嫦娥”携“玉兔”落月两大航天工程。某航天受好者提出“玉兔”回家的设想:如图,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球。设“玉兔”质量为m,月球为R,月面的重力加速度为g月。以月面为零势能面。“玉兔”在h高度的引力势能可表示为
正确答案
解析
略
知识点
如图,可视为质点的小球A、B用不可伸长的细软轻线连接,跨过固定在地面上、半径为R的光滑圆柱,A的质量为B的两倍。当B位于地面时,A恰与圆柱轴心等高。将A由静止释放,B上升的最大高度是 ( )
正确答案
解析
当A临落地时,根据动能定理:





知识点
扫码查看完整答案与解析