- 电磁感应中的能量转化
- 共184题
正方形导体框处于匀强磁场中,磁场方向垂直框平面,磁感应强度随时间均匀增加,变化率为k。导体框质量为m、边长为L,总电阻为R,在恒定外力F作用下由静止开始运动。导体框在磁场中的加速度大小为____________;导体框中感应电流做功的功率为____________。
正确答案
F/m;
k2L4/R
解析
加速度




知识点
如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”型导轨,在“U”型导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,且磁感应强度随时间变化规律如图乙所示。在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.1Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响(取g=10m/s2)。
(1)通过计算分析4s内导体棒的运动情况;
(2)计算4s内回路中电流的大小,并判断电流方向;
(3)计算4s内回路产生的焦耳热。
正确答案
见解析。
解析
(1)导体棒先在无磁场区域做匀减速运动,有
代入数据解得:
导体棒在1s末已经停止运动,以后一直保持静止,离左端位置仍为
(2)前2s磁通量不变,回路电动势和电流分别为
后2s回路产生的电动势为
回路的总长度为
电流为
根据楞次定律,在回路中的电流方向是顺时针方向。
(3)前2s电流为零,后2s有恒定电流,焦耳热为
知识点
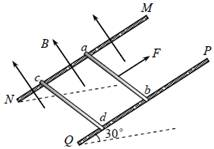
如图所示,两根足够长的光滑金属导轨MN、PQ间距为l=0.5m,其电阻不计,两导轨及其构成的平面均与水平面成30°角。完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终有良好接触,已知两棒的质量均为0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度为B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能保持静止。取g=10m/s2,问:
(1)通过cd棒的电流I是多少,方向如何?
(2)棒ab受到的力F多大?
(3)棒cd每产生Q=0.1J的热量,力F做的功W是多少?
正确答案
见解析。
解析
(1)棒cd受到的安培力 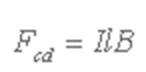
棒cd在共点力作用下平衡,则 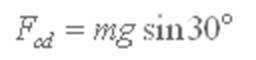
由①②式代入数据解得 I=1A,方向由右手定则可知由d到c。
(2)棒ab与棒cd受到的安培力大小相等 Fab=Fcd
对棒ab由共点力平衡有 
代入数据解得 F=0.2N④
(3)设在时间t内棒cd产生Q=0.1J热量,由焦耳定律可知 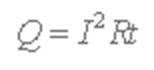
设ab棒匀速运动的速度大小为v,则产生的感应电动势 E=Blv ⑥
由闭合电路欧姆定律知 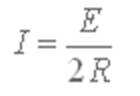
由运动学公式知,在时间t内,棒ab沿导轨的位移 x=vt⑧
力F做的功 W=Fx⑨
综合上述各式,代入数据解得 W=0.4J
知识点
如图,宽度为L=0.5m的光滑金属框架MNPQ固定于水平面内,并处在磁感应强度大小B=0.4T,方向竖直向下的匀强磁场中,框架的电阻非均匀分布,将质量m=0.1kg,电阻可忽略的金属棒ab放置在框架上,并与框架接触良好,以P为坐标原点,PQ方向为x轴正方向建立坐标,金属棒从x0=1m处以v0=2m/s的初速度,沿x轴负方向做a=2m/s2的匀减速直线运动,运动中金属棒仅受安培力作用,求:
(1)金属棒ab运动0.5m,框架产生的焦耳热Q;
(2)框架中aNPb部分的电阻R随金属棒ab的位置x变化的函数关系;
(3)为求金属棒ab沿x轴负方向运动0.4s过程中通过ab的电量q,某同学解法为:先算出经过0.4s金属棒的运动距离s,以及0.4s时回路内的电阻R,然后代入q=

正确答案
(1)金属棒ab运动0.5m,框架产生的焦耳热Q是0.1J;
(2)框架中aNPb部分的电阻R随金属棒ab的位置x变化的函数关系是R=0.4
(3)错误之处是把0.4s时回路内的电阻R代入q=
解析
(1)通过受力分析得:
金属棒仅受安培力作用,其大小F=ma=0.2N,
金属棒运动0.5m,因为安培力做功量度外界的能量转化成电能
所以框架中间生的焦耳热等于克服安培力做的功,
所以Q=Fs=0.1J。
(2)金属棒所受安培力为F=BIL,
感应电流I=

F=
由于棒做匀减速运动,根据运动学公式得:v=
所以R=

(3)错误之处是把0.4s时回路内的电阻R代入q=

知识点
如图17所示,质量为M的导体棒ab,垂直放在相距为l的平行光滑金属轨道上。导轨平面与水平面的夹角为θ,并处于磁感应强度大小为B.方向垂直与导轨平面向上的匀强磁场中,左侧是水平放置.间距为d的平行金属板R和Rx分别表示定值电阻和滑动变阻器的阻值,不计其他电阻。
(1)调节Rx=R,释放导体棒,当棒沿导轨匀速下滑时,求通过棒的电流I及棒的速率v。
(2)改变Rx,待棒沿导轨再次匀速下滑后,将质量为m.带电量为+q的微粒水平射入金属板间,若它能匀速通过,求此时的Rx。
正确答案
见解析。
解析
(1)当ab匀速运动时 列力平衡方程得:Mgsinθ=BIl①
ab切割产生的电动势为:E=Blv②
由闭合欧姆定律得:
由①②③得:
(2)再次平衡时有:
Mgsinθ=BIl
由闭合欧姆定律得:
对微粒列平衡方程得:Eq=mg ⑥
U=IRx ⑦
由④——⑦得:
知识点
扫码查看完整答案与解析